はじめに †
この資料は、「基礎から学ぶ実践データサイエンス」の第5週「機械学習の基礎」の資料です。
工学研究科情報工学専攻と生命健康科学研究科生命医科学専攻対象の「バイオインフォマティクス特論」(秋学期)の資料をまとめたもので、『Rによるバイオインフォマティクスデータ解析』を参考にしています。

準備 †
Rのインストールについては、次のページを見てください。
ここでは、標準で使用できるirisデータセットを使います。
> data(iris)
このデータセットは、アヤメの種類 (Species) をがく片の長さ (Sepal.Length)、幅 (Sepal.Width)、花びらの長さ (Petal.Length)、幅 (Petal.Width) によって分類する問題です。 長さと幅は連続値、種類はsetosa, versicolor, virginicaのいずれかをとる離散値です。
このデータセットには、setosa, versicolor, virginicaという3種類のアヤメについて、それぞれ50個ずつ、合計150個のデータが含まれています。 ランダムに10個のデータを選択して、見てみましょう。
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
機械学習 †
AIにおいては、「あるタスクについて、評価尺度 [math]E[/math] があるとき、機械(コンピューター)のが何らかの方法によって評価尺度 [math]E[/math] を向上させること」を機械学習 (machine learning) といいます。
データサイエンスにおいては、もう少し簡単に、「入力 [math]X[/math] と出力 [math]y[/math] の組 [math](X, y)[/math] を事例といい、事例の集合 [math]D[/math] が与えられたときに、[math]D[/math] から $$y_i = f(X_i) \qquad \forall (X_i, y_i) \in D$$ となる関数 [math]f[/math] を求めること」を機械学習といいます。
与えられた事例の集合 [math]D[/math] に出力 [math]y[/math] が含まれていないものを教師なし学習 (unsupervised learning) といい、出力 [math]y[/math] が含まれているものを教師あり学習 (supervised learning) といいます。
上のirisデータセットの場合、Sepal.Length, Sepal.Width, Petal.Length, Petal.Width を入力 [math]X[/math]、Species を出力 [math]y[/math] とすると、がく片の長さ、幅、花びらの長さ、幅からアヤメの種類を判別する教師付き学習と考えることができます。
教師なし学習 †
教師なし学習の代表的な手法は、与えられた事例をいくつかのグループに分割するクラスター分析(クラスタリング, clustering'')です。 クラスタリングの代表的な手法として、階層クラスタリング (hierarchical clustering) や [math]k[/math]-平均法 ([math]k[/math]-means) などありますが、ここでは階層クラスタリングを紹介します。
階層クラスタリングの代表的な方法の一つである凝集型階層クラスタリング (agglomerative hierarchical clustering) では、まず、1つのデータだけを含むクラスターをデータと同じ数だけ作ります。 それから、最も近い(似ている)クラスター同士を結合してより大きい新しいクラスターを作ります。 これを全てのクラスターが一つに結合されるまで繰り返します。
Rで階層クラスタリングを用いるには、hclust関数を用います。 hclust関数の引数には距離行列を与えます。 距離行列は、dist関数で求めることができます。
そこで、まず、irisデータのSepal.Length, Sepal.Width, Petal.Length, Petal.Widthの値から、距離行列を計算します。
> d <- dist(iris[,1:4])
この距離行列を用いて、階層クラスタリングを行います。
> hc <- hclust(d)
結果をplot関数を用いてプロットするとデンドログラム (dendrogram) と呼ばれる図が描かれます。
> plot(hc, labels=iris[,5], xlab="Iris")
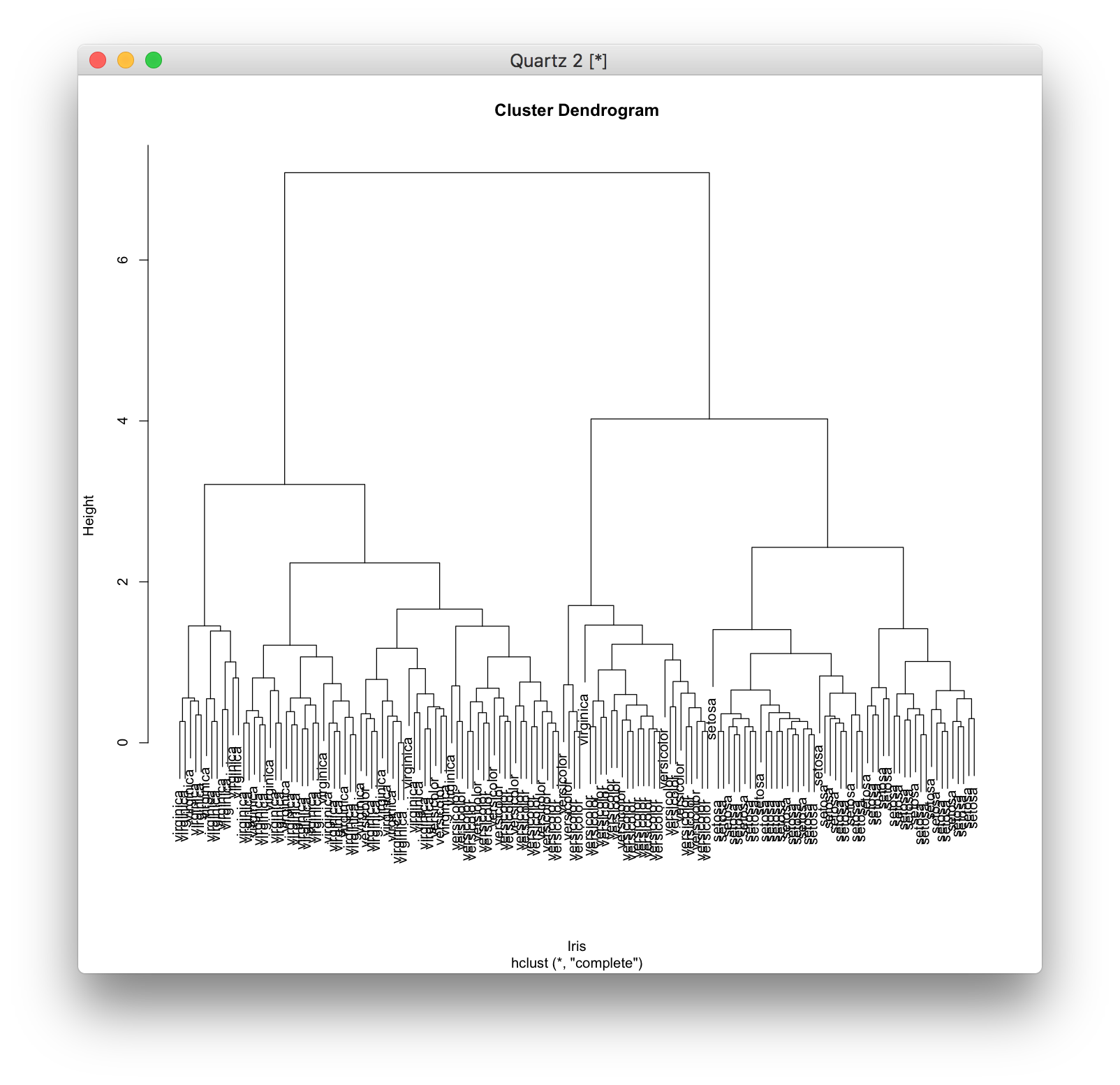
デンドログラムを見ると、どのクラスターが結合したのかがわかります。
距離尺度とクラスターを結合する方法にはいくつかの方法があります。 距離尺度には ユークリッド距離 (Euclidean distance)、結合方法にはWard法 (Ward method) がよく用いられます。
Ward法は、クラスター[math]C_1, C_2[/math]を結合してクラスター[math]C_1 \cup C_2[/math]を作ったときに、各データとそれが含まれるクラスターの重心との距離の分散の増分を[math]C_1 C_2[/math]間の距離として、最も近い(似ている)クラスターを結合します。 \[ d(C_1, C_2) = {\mathrm E}(C_1 \cup C_2) - {\mathrm E}(C_1) - {\mathrm E}(C_2) \] \[ {\mathrm E}(C_i) = \sum_{{\bf x} \in C_i} (d({\bf x}, {\bf c_i}))^2 \] Ward法を用いるには、hclust関数にオプションmethod="ward.D"を指定します(新しい ward.D2 という方法もあります)。
> d <- dist(iris[,1:4]) > hc <- hclust(d, method="ward.D") > plot(hc, labels=iris[,5], xlab="Euclidean")
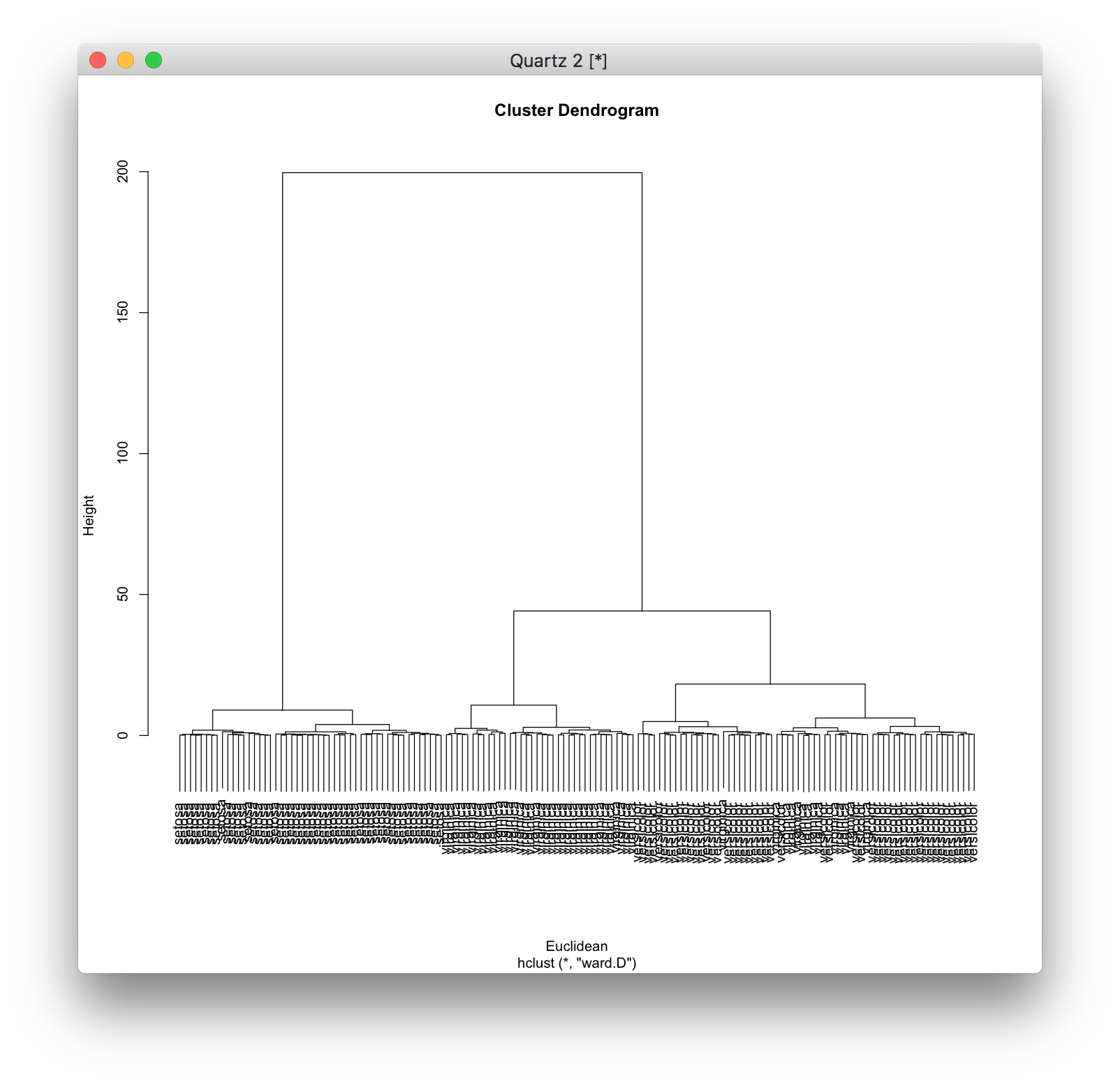
教師あり学習 †
出力 [math]y[/math] が与えられる教師あり学習において、[math]y[/math] が連続値(数値)であるものを回帰分析 (regression) といい、離散値(カテゴリー)であるものをカテゴリー分析 (categolization) または分類分析 (classification) といいます。
回帰分析 †
単回帰分析 †
説明したい値を目的変数といい、目的変数を説明するために使う変数を説明変数と言います。 統計の分野では、目的変数を従属変数、説明変数を独立変数と呼びます。
まず、説明変数が1つの単回帰(single linear regression)を行います。 つまり、モデルが次のような式で表される直線をデータから求めます。 \[\hat{y} = \beta_0 + \beta_1 x_1\] ここで、[math]\hat{y}[/math]がモデルによる予測値、[math]x_1[/math]が説明変数、[math]\beta_0[/math]が定数項、[math]\beta_1[/math]が([math]x_1[/math]の)係数です。
ある観測値 [math](x_i, y_i)[/math] に対して、モデルの予測値 [math]\hat{y_i}[/math] と観測値 [math]y_i[/math] の差を残差といい、次の式で表されます。 \[ y_i - \hat{y_i} = y_i - (\beta_0 + \beta_1 x_{i, 1}) \]
線形回帰では、残差の二乗の和を最小化するような係数と定数項を最小二乗法を使って求めます。 つまり、単回帰では、[math]N[/math] 個の観測データに対して、次の値を最小化するよう [math]\beta_0[/math]と [math]\beta_1[/math] を求めます。 (求め方の説明は省きます。) \[ \sum_{i=1}^N \left(y_i - (\beta_0 + \beta_1 x_{i,1})\right)^2 \]
例として、がくの長さ(Petal.Length)を横軸、花びらの長さ(Sepal.Length)を縦軸にとって、150個のデータをプロットしてみます。
plot(iris$Sepal.Length, iris$Petal.Length)
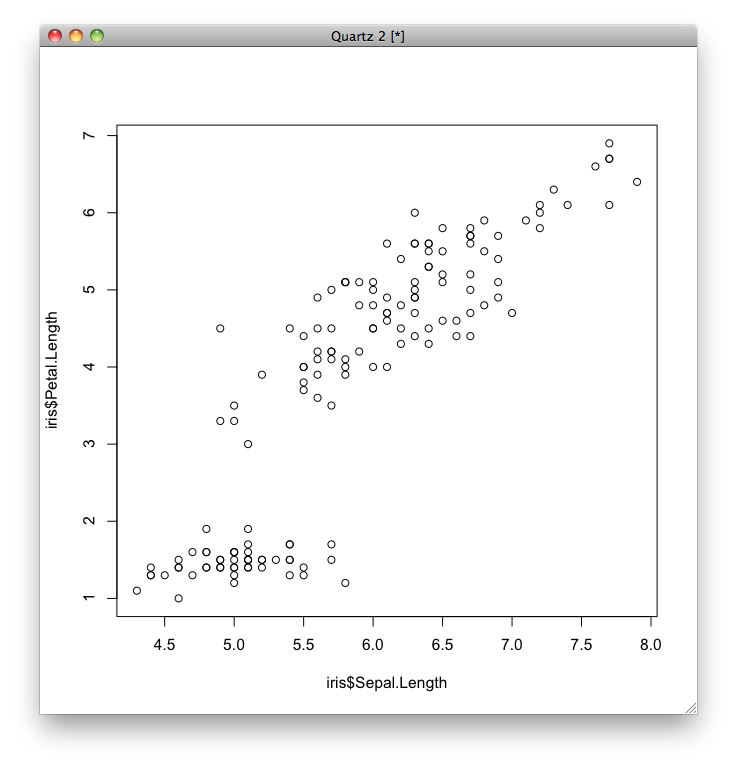
どうやら、花びらの長さとがくの長さの間には正の相関(一方が大きいと他方も大きいという関係)がありそうですね。 そこで、花びらの長さ(Sepal.Length)を [math]x_1[/math](説明変数)、がくの長さ(Petal.Length)を [math]y[/math](目的変数)として、単回帰を行いましょう。
Rでは、モデルの式を、記号~を使って「目的変数 ~ 説明変数」というように表します。 したがって、目的変数 [math]y[/math] をがくの長さ(Petal.Length)、説明変数 [math]x_1[/math] を花びらの長さ(Sepal.Length)とするとき、モデルの式は「y ~ x1」となります。
y <- iris$Petal.Length x1 <- iris$Sepal.Length
線形回帰は、標準で用意されているlm関数にモデル式を入力して行います。
iris.sgl <- lm(y ~ x1)
学習された結果を表示してみると、次のようになります。
iris.sgl
Call: lm(formula = y ~ x1) Coefficients: (Intercept) x1 -7.101 1.858
Coefficientsは係数を表し、Interceptは定数項の値(切片)を表します。 つまり、花びらの長さを [math]x_1[/math]、がくの長さを [math]y[/math] とすると、学習された式は次のように書けます。 \[ y = -7.101 + 1.858 x_1 \]
学習された単回帰モデルを図示します。
plot(x1, y) abline(iris.sgl)
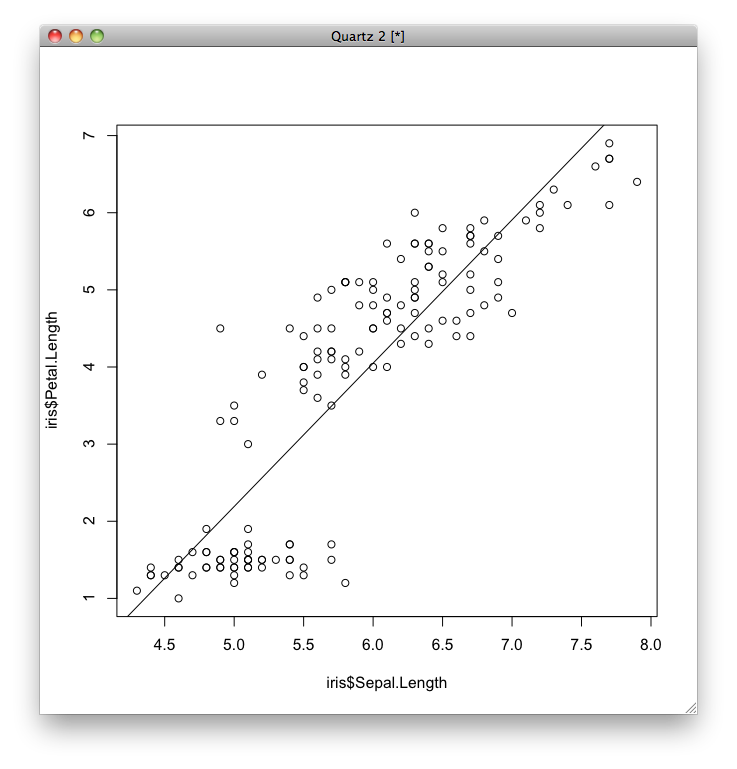
学習されたモデルをsummary関数に渡すと、モデルに関する情報のサマリーが出力されます。
summary(iris.sgl)
Call: lm(formula = y ~ x1) Residuals: Min 1Q Median 3Q Max -2.47747 -0.59072 -0.00668 0.60484 2.49512 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -7.10144 0.50666 -14.02 <2e-16 *** x1 1.85843 0.08586 21.65 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.8678 on 148 degrees of freedom Multiple R-squared: 0.76, Adjusted R-squared: 0.7583 F-statistic: 468.6 on 1 and 148 DF, p-value: < 2.2e-16
Residualsは、残差の最小値、中央値、最大値、四分位数を表します。
Coefficientsは、切片 (Intercept) [math]\beta_0[/math] と [math]x_1[/math] の係数 [math]\beta_1[/math] の推定値 (Estimate)、標準誤差 (Std. Error)を表します。
また、それぞれの推定値が 0 であるという帰無仮説に対するt検定のt統計量 (t value)、p値 (Pr(>|t|)) が示されています。 p値が0.05を超えている場合は、その説明変数は有意水準5%で統計的に有意ではなく、使えないと判断します。
Multiple R-squaredは、決定係数で、このモデルがどのくらい説明できているかを 0 から 1 の範囲で表します。
単回帰では説明変数を1つしか使いませんが、説明変数を複数使うことができ、説明変数を増やすと決定係数を1に近づけることができてしまいます。 Adjusted R-squaredは、自由度調整済み決定係数で、説明変数の数(自由度)によって調整した決定係数を表します。 説明変数の数が異なるモデルを比較するときには、自由度調整済み決定係数を使います。
最後に、係数が全て 0 であるという帰無仮説に対するF検定のF統計量 (F-statistic) とp値 (p-value) が示されています。 p値が0.05を超えている場合は、このモデルは有意水準5%で統計的に有意ではなく、使えないと判断します。
次に、予測誤差を視覚化するため、それぞれのデータについて、横軸に実際のがくの長さ(Petal.Length)、縦軸にその予測値をとってグラフを表示します。 予測値はpredict関数で求めることができます。
plot(y, predict(iris.sgl)) abline(a=0,b=1)
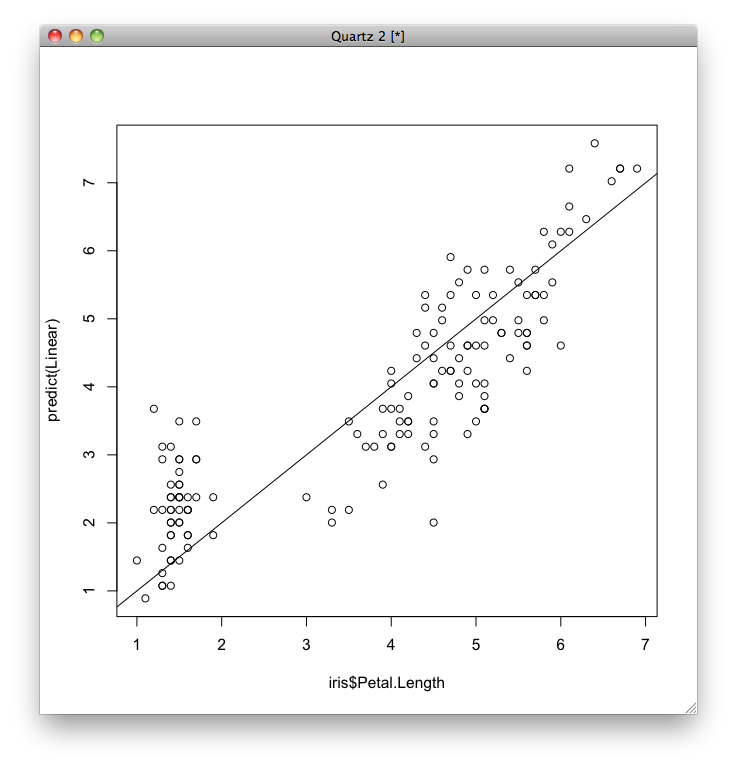
この予測がどのくらい良いのかを表すために、平均二乗誤差(実際の値と予測値の差の二乗の平均)を求めます。 \[\textit{MSE} = \frac{1}{N}\sum_{i=1}^{N} \left(y_i - (\beta_0 + \beta_1 x_{i,1})\right)^2\]
mean((y - predict(iris.sgl))**2)
[1] 0.743061
重回帰分析 †
説明変数が複数ある線形回帰を重回帰(multiple linear regression)といいます。
重回帰のモデルは次のような式で表されます。 \[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p\ = \beta_0 + \beta^\mathrm{T}\bf{x}\] ここで、[math]\beta[/math]と[math]\bf{x}[/math]は、それぞれ[math]\beta_1, \dots, \beta_p[/math]と[math]x_1, \dots, x_p[/math]を要素とするベクトルです。
また、単回帰のときと同様に、次式で表される二乗誤差の総和を最小化するような[math]\beta_0, \dots, \beta_p[/math]を求めます。 \[\sum_{i=1}^N \left(y_i - (\beta_0 + \beta^\mathrm{T}\bf{x}_i)\right)^2\]
ここでは、がくの長さ(Petal.Length)を目的変数 [math]y[/math]、花びらの長さ(Sepal.Length)、幅(Sepal.Width)、がくの幅(Petal.Width)を説明変数 [math]x_1[/math], [math]x_2[/math], [math]x_3[/math] として重回帰を行いましょう。
y <- iris$Petal.Length x1 <- iris$Sepal.Length x2 <- iris$Sepal.Width x3 <- iris$Petal.Width
説明変数が複数あるときは、モデルを表すときにそれぞれの変数を記号+で連結して表します。 ここでは、「y ~ x1+x2+x3」となります。
単回帰と同じように、lm関数を用いてモデルを学習します。
iris.mult <- lm(y ~ x1+x2+x3) iris.mult$coefficients
(Intercept) x1 x2 x3 -0.2627112 0.7291384 -0.6460124 1.4467934
単回帰と同じように、学習された式は次のように書けます。 \[ y = -0.2627112 + 0.7291384 x_1 - 0.6460124 x_2 + 1.4467934 x_3 \]
単回帰と同じように、学習されたモデルをsummary関数に渡すと、モデルに関する情報のサマリーが出力されます。
summary(iris.mult)
Call: lm(formula = y ~ x1 + x2 + x3) Residuals: Min 1Q Median 3Q Max -0.99333 -0.17656 -0.01004 0.18558 1.06909 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.26271 0.29741 -0.883 0.379 x1 0.72914 0.05832 12.502 <2e-16 *** x2 -0.64601 0.06850 -9.431 <2e-16 *** x3 1.44679 0.06761 21.399 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.319 on 146 degrees of freedom Multiple R-squared: 0.968, Adjusted R-squared: 0.9674 F-statistic: 1473 on 3 and 146 DF, p-value: < 2.2e-16
重回帰分析の場合はモデルが視覚化しにくいので、予測誤差だけ視覚化します。
plot(y, predict(iris.mult)) abline(a=0,b=1)
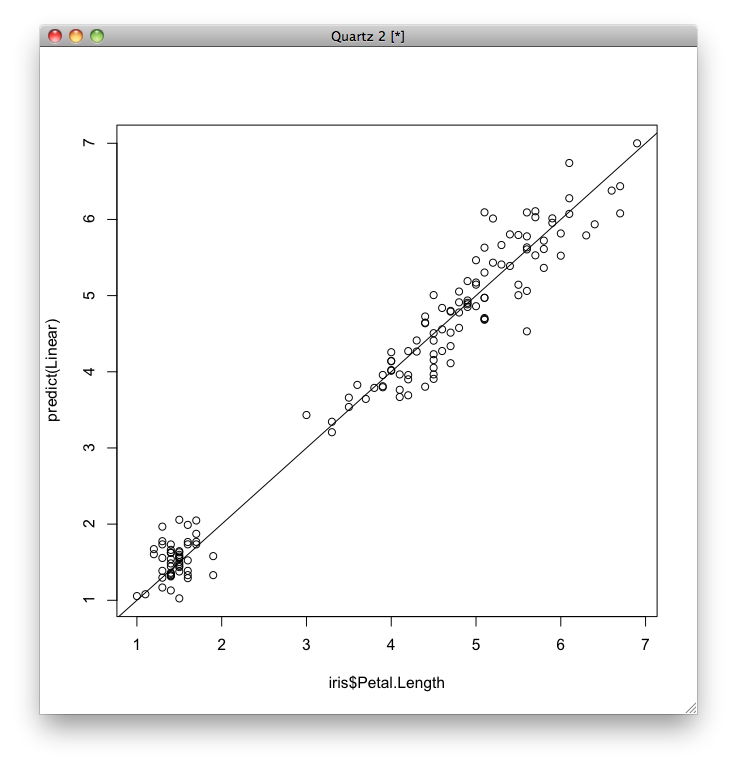
単回帰と同様に、平均二乗誤差を求めます。 \[\textit{MSE} = \frac{1}{N} \sum_{i=1}^N (y_i - (\beta_0 + \beta^\mathrm{T}\bf{x}_i))^2\]
mean((y - predict(iris.mult))**2)
[1] 0.09901965
単回帰の場合よりも誤差がかなり小さくなっていることがわかります。
カテゴリー分析 †
出力 [math]y[/math] が離散値(カテゴリー)であるカテゴリー分析(分類分析)の基礎的な手法に決定木学習 (decision tree) があります。
Rで決定木学習を行うには、treeパッケージ*1*2を使います. install.packagesコマンドを入力すると,パッケージをダウンロードするサーバーを聞かれますので,リストからJapanを選択します.
install.packages("tree") library(tree)
決定木学習は、説明変数に対する条件を用いて事例集合を分割することによってラベル(カテゴリー)を予測するための決定木を学習するものです。 実物を見た方が理解しやすいので早速決定木を学習します。
まず、treeコマンドを用いて決定木を学習します。
iris.tree <- tree(Species ~ ., iris)
ここで、第1引数の「Species ~ .」はモデル式、第2引数の「iris」は訓練データを表しています。 モデル式は「目的変数 ~ 説明変数」という形で表現し、説明変数が「.」(ドット)のときは、目的変数以外の全ての変数を表します。 したがって、ここでは、irisデータセットのSpeciesを目的変数とし、それ以外のすべての変数(Spepal.Lenght, Sepal.Width, Petal.Length, Petal.Width)を説明変数としています。
次に、学習された決定木を表示します。
iris.tree
node), split, n, deviance, yval, (yprob) * denotes terminal node 1) root 150 329.600 setosa ( 0.33333 0.33333 0.33333 ) 2) Petal.Length < 2.45 50 0.000 setosa ( 1.00000 0.00000 0.00000 ) * 3) Petal.Length > 2.45 100 138.600 versicolor ( 0.00000 0.50000 0.50000 ) 6) Petal.Width < 1.75 54 33.320 versicolor ( 0.00000 0.90741 0.09259 ) 12) Petal.Length < 4.95 48 9.721 versicolor ( 0.00000 0.97917 0.02083 ) 24) Sepal.Length < 5.15 5 5.004 versicolor ( 0.00000 0.80000 0.20000 ) * 25) Sepal.Length > 5.15 43 0.000 versicolor ( 0.00000 1.00000 0.00000 ) * 13) Petal.Length > 4.95 6 7.638 virginica ( 0.00000 0.33333 0.66667 ) * 7) Petal.Width > 1.75 46 9.635 virginica ( 0.00000 0.02174 0.97826 ) 14) Petal.Length < 4.95 6 5.407 virginica ( 0.00000 0.16667 0.83333 ) * 15) Petal.Length > 4.95 40 0.000 virginica ( 0.00000 0.00000 1.00000 ) *
テキストでは分かりにくいので、図にします。
plot(iris.tree) text(iris.tree)

一番上が根(root)と呼ばれます。 根から枝(branch)が下へと伸び、節(node)で分岐します。 節は条件に対応します。 枝の先端が葉(leaf)で、葉はカテゴリー(ラベル)に対応します。
最初に、根の条件「Petal.Lengthの値が2.45より小さいか」によって事例を分けます。 Petal.Lengthの値が2.45よりも小さい事例は左に、そうでない事例は右に振り分けられます。 右に振り分けられた事例は、次に、2番目の条件「Petal.Widthの値が1.75より小さいか」によって振り分けられます。 Petal.Widthの値が1.75よりも小さい事例は左に、そうでない事例は右に振り分けられます。
ここで右に振り分けられた事例は、「Petal.Lengthの値が2.45より大きい」かつ「Petal.Widthの値が1.74より大きい」事例です。 このように、決定木は、論理積(かつ)で結合した条件を表しています。
先に表示したテキストで見てみましょう。
最初の条件で分割する前の集合は 1) です。 最初のrootのところは条件を表しますが、ここでは条件がないのでrootと書かれています。 150はこの集合に含まれる事例の数、239.600はこの集合に含まれる事例のバラツキの度合いです。 そしてsetosaはこの集合に振り分けられた事例に対する予測ラベルです。 ( 0.33333 0.33333 0.33333 )は、setosa, versicolor, virginicaの出現確率を表しています。
最初の条件は「Petal.Length < 2.45」です。 この条件に当てはまる事例の集合が 2) で、そうでない事例の集合が 3) です。 このような分割が葉に至るまで続きます。
ここで、図の右下の条件を見ると、「Petal.Length < 4.95」という条件で分割していますが、どちらに振り分けられてもvirginicaと予測されています。 同じように、左下の条件でも左右ともversicolorになっています。 前者の集合は 7)、後者の集合は 12) です。
そこで、この条件を決定木から取り除きます。 これを枝刈りといいます。 枝刈りをするには、snip.tree関数を使って、nodeオプションに枝刈りする(条件分岐を止める)節番号のベクトルを指定します。
iris.tree.snip <- snip.tree(iris.tree, nodes=c(7,12)) plot(iris.tree.snip) text(iris.tree.snip)
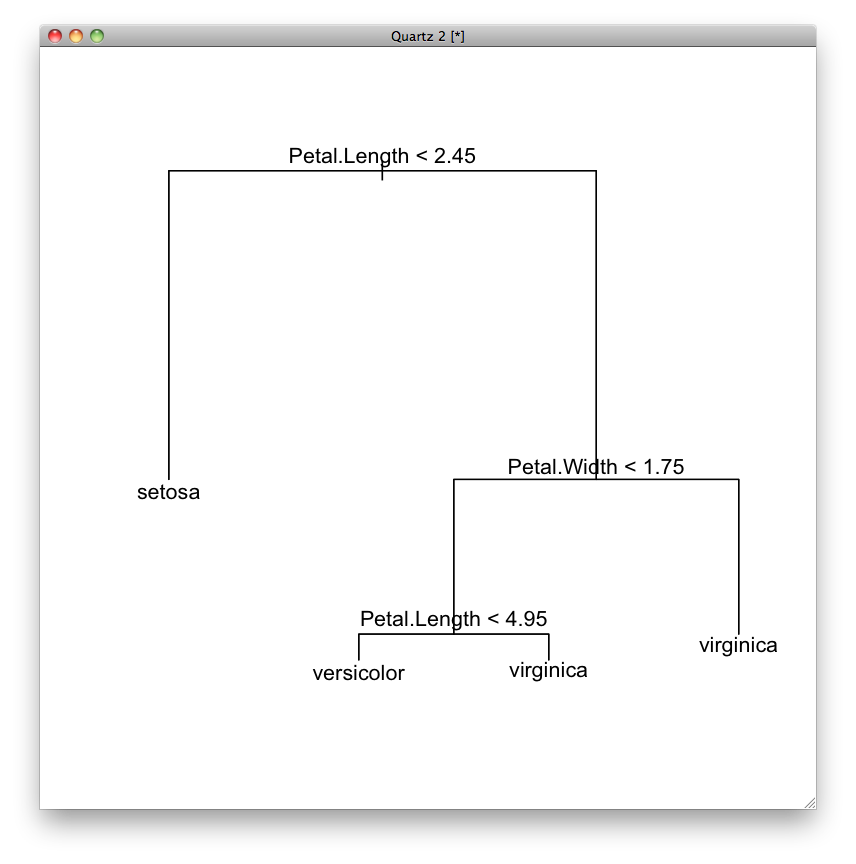
iris.tree.snip
node), split, n, deviance, yval, (yprob) * denotes terminal node 1) root 150 329.600 setosa ( 0.33333 0.33333 0.33333 ) 2) Petal.Length < 2.45 50 0.000 setosa ( 1.00000 0.00000 0.00000 ) * 3) Petal.Length > 2.45 100 138.600 versicolor ( 0.00000 0.50000 0.50000 ) 6) Petal.Width < 1.75 54 33.320 versicolor ( 0.00000 0.90741 0.09259 ) 12) Petal.Length < 4.95 48 9.721 versicolor ( 0.00000 0.97917 0.02083 ) * 13) Petal.Length > 4.95 6 7.638 virginica ( 0.00000 0.33333 0.66667 ) * 7) Petal.Width > 1.75 46 9.635 virginica ( 0.00000 0.02174 0.97826 ) *
学習した決定木を使って、カテゴリー(Species)が未知のデータに対してそのカテゴリーを予測してみましょう。
まず、data.frame関数を用いてデータ・フレームを作成します。
testdata <- data.frame( Sepal.Length=c(6.2,7.0,5.0), Sepal.Width=c(3.3,3.3,3.5), Petal.Length=c(6.0,4.5,1.4), Petal.Width=c(2.4,1.4,0.3) ) testdata
Sepal.Length Sepal.Width Petal.Length Petal.Width 1 6.2 3.3 6.0 2.4 2 7.0 3.3 4.5 1.4 3 5.0 3.5 1.4 0.3
次に、predict関数を用いてカテゴリーを予測します。
predict(iris.tree, testdata)
setosa versicolor virginica 1 0 0 1 2 0 1 0 3 1 0 0
1番目の事例はvirginicaに、2番目の事例はversicolorに、3番目の事例はsetosaと予測されました。
また、枝刈りされた決定木を用いて予測すると次のようになります。
predict(iris.tree.snip, testdata)
setosa versicolor virginica 1 0 0.02173913 0.97826087 2 0 0.97916667 0.02083333 3 1 0.00000000 0.00000000
1番目の事例は97.8%の確率でvirginicaに、2.2%の確率でversicolorに分類されると予測されました。 同様に、2番目の事例は97.9%の確率でversicolorに、2.1%の確率でverginicaに分類されると予測されました。 3番目の事例は枝刈りしなかったときと同様に100%の確率でsetosaと予測されました。
まとめ †
データサイエンスにおける機械学習は、出力 [math]y[/math] が与えられない教師なし学習と与えられる教師あり学習に分けられます。
教師なし学習の代表的な手法はクラスタリングであり、代表的なクラスタリングの手法として凝集型階層クラスタリングがあります。
教師あり学習のうち、出力 [math]y[/math] が連続値(数値)であるものを回帰分析、離散値(カテゴリー)であるものをカテゴリー分析または分類分析といいます。 回帰分析の代表的な手法には重回帰分析があり、カテゴリー分析の基礎的な手法には決定木学習があります。
自分の分析の目的に応じて適切に手法を使い分けることが重要です。
課題 †
irisデータセットを用いて、クラスター分析、重回帰分析、決定木学習を自分で行え。
レポートには、自分が実行したコマンド、その出力結果、結果についての簡潔な説明を示すこと。
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)