Pythonでデータ分析する次の一歩（ディープ・ラーニング、Keras編）

はじめに †

Kerasはディープ・ラーニング・ライブラリーのTensorFlowを使用するためのライブラリーです。

この内容は、Keras 2.2.4で確認しました。

インストール †

ここでは、Anacondaに追加する形でインストールします。

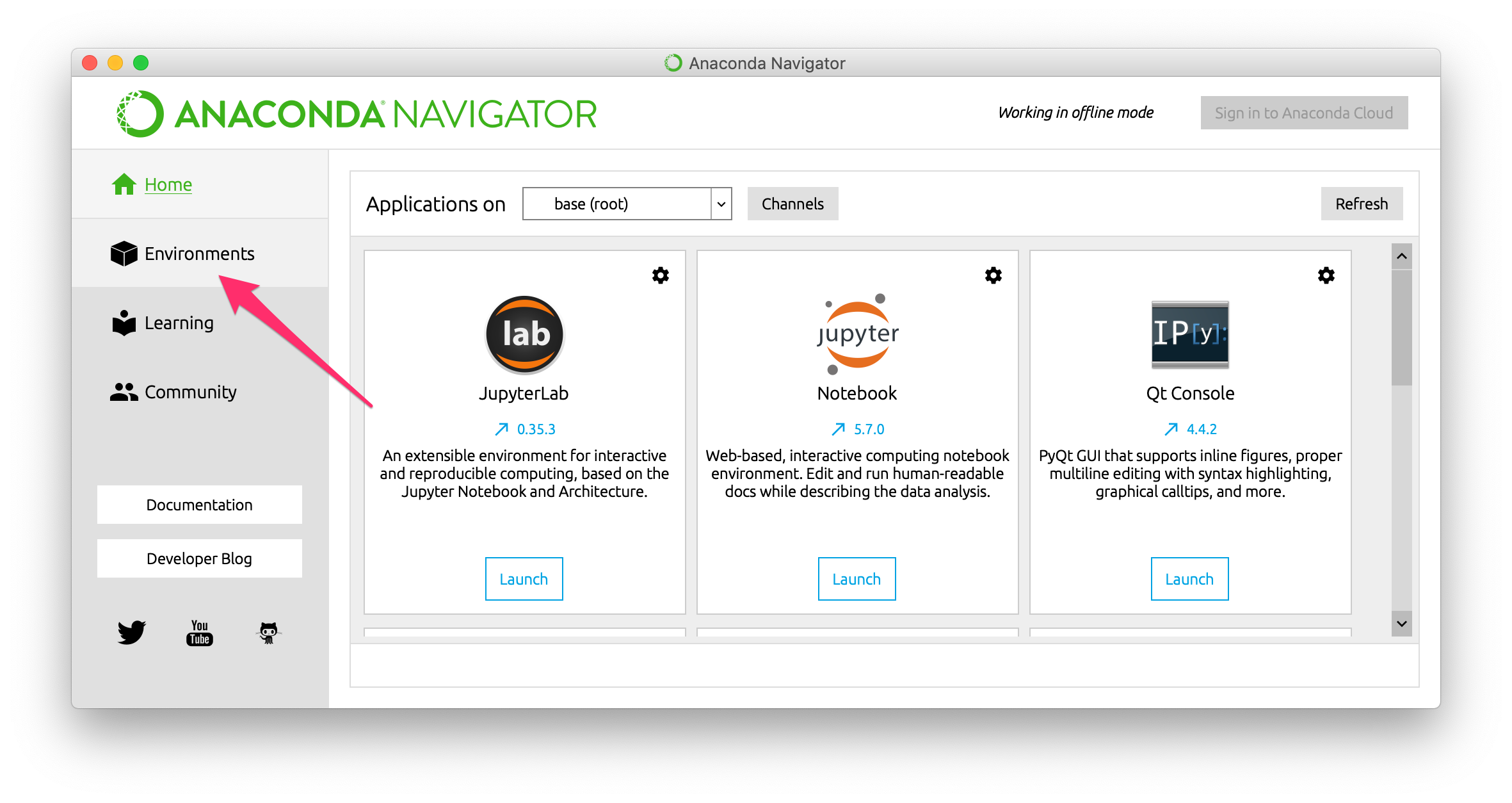
まず、Anaconda Navigatorを起動し、Environmentsを表示します。

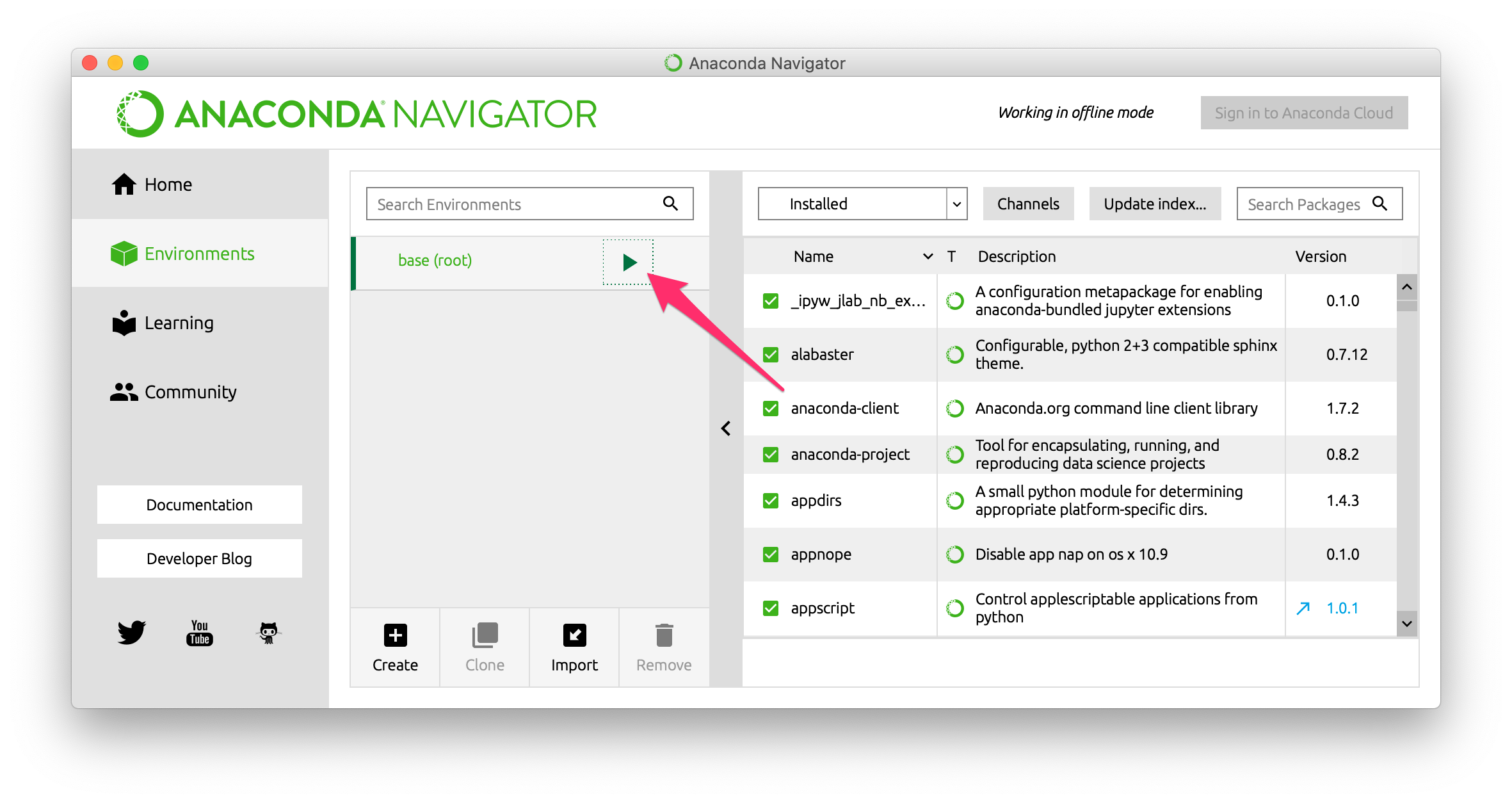
次に、base (root)の横の三角形をクリックし、メニューを表示します。

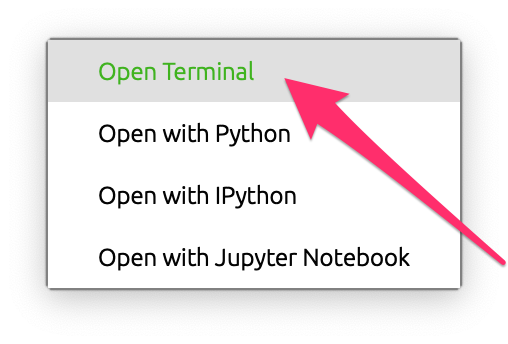
メニューから、Open Terminalを選び、ターミナルを開きます。

ターミナルを開いたら、念の為、CondaとMatplotlibをアップデートします。

conda update conda
conda update matplotlib

CondaとMatplotlibをアップデートしたら、Kerasをインストールします。 TensorFlowはKerasと一緒にインストールされます。

conda install keras

使い方 †

ライブラリーの読み込み †

ライブラリー名は keras です。

import keras

ライブラリーを読み込んで、次のようなメッセージが出てきたら、準備はできています。

Using TensorFlow backend.

バージョンを確認する方法はこちらです。

print(keras.__version__)

データの準備 †

まず、scikit-learnに付属しているIrisデータセットを例題として使います。 説明変数は花びらの長さ、幅、萼（がく）片の長さ、幅の4つ、目的変数はSetosaを表す0、Versicolorを表す1、Virginicaを表す2の3種類です。

from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
print(X)
print(y)

[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 ...
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

説明変数が4つあることから、入力層のユニット数は4になります。 目的変数が3種類あることから、出力層のユニット数は3になります。

ただし、分類器の予測モデルでは、目的変数はOne hotベクトルにしておく必要があります。

Kerasに、One hotベクトルに変換するためのto_categoricalメソッドが用意されています。

from keras.utils import np_utils
y = np_utils.to_categorical(y)
print(y)

[[1. 0. 0.]
 [1. 0. 0.]
 [1. 0. 0.]
 ...
 [0. 0. 1.]
 [0. 0. 1.]
 [0. 0. 1.]]

予測モデル学習器の生成 †

Kerasを使うことで、ディープ・ラーニング・ライブラリーのTensorFlowをscikit-learnと同じように使えます。

ディープ・ラーニングというのは、ニューラル・ネットワークの中間層が2つ以上のものです。 ここでは、基本的な全結合の4層モデル（入力層、中間層2つ、出力層）を作成する例を示します。

まず、シーケンシャル・モデルの入れ物を作成します。

from tensorflow.keras.models import Sequential
model = Sequential()

次に、入力層と1つ目の中間層を追加します。

from tensorflow.keras.layers import Dense
model.add(Dense(units=16, activation='relu', input_dim=4))

Dense は全結合のレイヤーです。 units はこのレイヤーのユニット数、activation は活性化関数（ここではランプ関数 ReLU）を表します。 input_dim オプションは入力層のユニット数を表し、最初の中間層だけに指定します。 説明変数が4つなので、入力層のユニット数は4です。

続いて、2つ目の中間層を追加します。

model.add(Dense(units=8, activation='relu'))

最後に、出力層を追加します。

model.add(Dense(units=3, activation='softmax'))

分類用なので、出力層の活性化関数をソフトマックスにしています。 出力が3種類なので、出力層のユニット数は3です。 （回帰用の場合は、出力層の活性化関数を線形 activation='linear' にします。）

全てのレイヤーを追加したら、モデルをコンパイルします。

model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])

loss は損失関数、optimizer は最適化手法、metrics は評価尺度を表します。 ここでは、分類用なので、損失関数はカテゴリカル・クロスエントロピー categorical_crossentropy、評価尺度は精度 accuracy にしています。 最適化手法は、最もシンプルな確率的勾配法 SGD にしています。

ニューラル・ネットワークの学習 †

scikit-learnと同じように、fitメソッドで学習します。

model.fit(X, y, epochs=1000, batch_size=150)

Train on 150 samples
Epoch 1/1000
150/150 [==============================] - 1s 8ms/sample - loss: 2.0354 - accuracy: 0.3333
Epoch 2/1000
150/150 [==============================] - 0s 42us/sample - loss: 1.8037 - accuracy: 0.3333
Epoch 3/1000
150/150 [==============================] - 0s 74us/sample - loss: 1.6263 - accuracy: 0.3333
Epoch 4/1000
150/150 [==============================] - 0s 64us/sample - loss: 1.4876 - accuracy: 0.3333
Epoch 5/1000
150/150 [==============================] - 0s 54us/sample - loss: 1.3778 - accuracy: 0.3333
...
Epoch 998/1000
150/150 [==============================] - 0s 43us/sample - loss: 0.1798 - accuracy: 0.9733
Epoch 999/1000
150/150 [==============================] - 0s 49us/sample - loss: 0.1794 - accuracy: 0.9733
Epoch 1000/1000
150/150 [==============================] - 0s 39us/sample - loss: 0.1791 - accuracy: 0.9733

epochs は事例全体に対して何回繰り返し学習するか、batch_size は重みの更新をいくつの事例ごとに行うかを表します。 Irisデータセットには事例が150個含まれているので、ここでは150事例ごとに1,000回重みを更新しています。 （batch_size=1 にすると、1事例ごとに、150,000回重みを更新します。）

学習した予測モデルの評価 †

scikit-learnと同じように、evaluateメソッドで評価します。

score = model.evaluate(X, y, batch_size=150)
print(model.metrics_names)
print(score)

150/1 [==========...
...=====] - 0s 1ms/sample - loss: 0.1787 - accuracy: 0.9733
['loss', 'accuracy']
[0.17870810627937317, 0.97333336]

ここでは、訓練データを用いて予測モデルを評価していますが、本来は、訓練データとは別に検証データを用意して評価します。

損失が0.179、精度が0.973でした。

学習した予測モデルによる予測 †

scikit-learnと同じように、predictメソッドで予測します。

model.predict(X)

array([[9.30257916e-01, 3.53016481e-02, 3.44404392e-02],
       [9.22631919e-01, 3.99531014e-02, 3.74150351e-02],
       [9.21679020e-01, 4.05398346e-02, 3.77811491e-02],
...
       [1.05547340e-04, 8.70669410e-02, 9.12827492e-01],
       [1.82199045e-04, 1.80615202e-01, 8.19202602e-01]], dtype=float32)

最後の活性化関数がsoftmax関数のため、ユニットごとに確率が出力されます。 つまり出力は150行3列の行列になります。

そこで、argmaxメソッドで行ごとに最大値を持つインデックス番号を求めます。

import numpy as np
p = np.argmax(model.predict(X), axis=1)
print(p)

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1
 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

畳み込みディープ・ニューラル・ネットワーク (CDNN) による画像分類 †

手書き文字認識のMNISTデータセットを用いて、畳み込みディープ・ニューラル・ネットワークを使って画像分類をやってみます。

まずはデータセットをダウンロドします。

from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()

Downloading data from https://s3.amazonaws.com/img-datasets/mnist.npz
11493376/11490434 [==============================] - 136s 12us/step

最初の100個のデータを表示してみます。

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(10, 10))
fig.subplots_adjust(left=0, right=1, bottom=0, top=0.5, hspace=0.1, wspace=-0.9)
for i in range(100):
    ax = fig.add_subplot(10, 10, i + 1, xticks=[], yticks=[])
    ax.imshow(X_train[i].reshape((28, 28)), cmap='gray')

訓練データには縦横28ピクセルのモノクロ画像が6万枚入っています。

print(X_train.shape)
print(y_train)

(60000, 28, 28)
[5 0 4 ... 5 6 8]

一般的な画像データはRGBなど複数のチャンネルを持っていますが、MNISTデータセットはモノクロ画像なので1チャンネルしかありません。 そのため、MNISTデータセットでは1つの画像が1つの行列だけで表現されています。 複数のチャンネルを持つ一般的な画像データは3階テンソルによって表されるため、MNISTデータセットを6万個の画像データ（3階テンソル）からなる4階テンソルに変形しておく必要があります。

そこで、訓練データを (画像枚数, 横ピクセル数, 縦ピクセル数, チャンネル数) という形に変形します。

X_train = X_train.reshape(60000, 28, 28, 1)

Irisデータセットと同じように、目的変数をOne hotベクトルに変換します。

from keras.utils import np_utils
y_train = np_utils.to_categorical(y_train)
print(y_train)

[[0. 0. 0. ... 0. 0. 0.]
 [1. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 1. 0.]]

データの準備ができたので、次はモデルを作成します。

from tensorflow.keras.models import Sequential
model = Sequential()

最初の畳み込み層を追加します。

from tensorflow.keras.layers import Conv2D
model.add(Conv2D(filters=32, kernel_size=(3, 3), activation='relu', input_shape=(28, 28, 1)))

Conv2D は2次元の畳み込み層です。 units は畳み込み層のユニット数、kernel_size は畳み込みカーネルのサイズです。 input_shape は入力の形 (横ピクセル数, 縦ピクセル数, チャンネル数) で、最初の畳み込み層にだけ指定します。

続いて、2層目の畳み込み層を追加します。

model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))

この後に、プーリング層を追加します。

from tensorflow.keras.layers import MaxPooling2D
model.add(MaxPooling2D(pool_size=(2, 2)))

MaxPooling2D は2次元のMaxプーリング層です。 pooling_size はプーリングのサイズを表します。

ここで、ドロップアウトします。

from tensorflow.keras.layers import Dropout
model.add(Dropout(rate=0.25))

Dropoutはドロップアウトを表現しています。 レイヤーと同じように追加されていますが、レイヤーではありません。 rate はドロップする割合を表します。

次に、特徴を1次元にします。

from tensorflow.keras.layers import Flatten
model.add(Flatten())

1次元にしたユニットから全結合した中間層を加え、ドロップアウトします。

from tensorflow.keras.layers import Dense
model.add(Dense(units=128, activation='relu'))
model.add(Dropout(rate=0.5))

最後に、出力層を追加します。

model.add(Dense(units=10, activation='softmax'))

10クラス分類問題なので出力層のユニット数は10、活性化関数はソフトマックスです。

全てのレイヤーを追加したら、コンパイルします。

model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

損失はカテゴリカル・エントロピー、最適化アルゴリズムはAdam、評価尺度は精度を指定します。

コンパイルしたら、学習します。（メモリーが不足しているとJupyter Notebookのカーネルが死にます。自分のPCでできないときは、Colaboratoryを使いましょう。）

model.fit(X_train, y_train, epochs=12, batch_size=128)

#geshi(sh){{
Train on 60000 samples
Epoch 1/12
60000/60000 [==============================] - 126s 2ms/sample - loss: 0.8976 - accuracy: 0.8477
Epoch 2/12
60000/60000 [==============================] - 134s 2ms/sample - loss: 0.1689 - accuracy: 0.9512
Epoch 3/12
60000/60000 [==============================] - 126s 2ms/sample - loss: 0.1232 - accuracy: 0.9639
Epoch 4/12
60000/60000 [==============================] - 127s 2ms/sample - loss: 0.1019 - accuracy: 0.9696
Epoch 5/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0910 - accuracy: 0.9725
Epoch 6/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0806 - accuracy: 0.9756
Epoch 7/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0742 - accuracy: 0.9777
Epoch 8/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0705 - accuracy: 0.9785
Epoch 9/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0620 - accuracy: 0.9812
Epoch 10/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0582 - accuracy: 0.9813
Epoch 11/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0547 - accuracy: 0.9827
Epoch 12/12
60000/60000 [==============================] - 125s 2ms/sample - loss: 0.0523 - accuracy: 0.9839}}

学習したら、評価します。

まず、テスト・データの形を確認します。

print(X_test.shape)

(10000, 28, 28)

訓練データと同じように、説明変数と目的変数を変形し、評価します。

X_test = X_test.reshape(10000, 28, 28, 1)
y_test = np_utils.to_categorical(y_test)
model.evaluate(X_test, y_test)

10000/1 [==========...
...=====] - 8s 803us/sample - loss: 0.0207 - accuracy: 0.9886
[0.04147466113096273, 0.9886]

損失は0.041、精度は0.989でした。

出力は10,000行10列の行列になるので、Irisデータセットのときと同じように、argmaxメソッドを使って行ごとに最大値のインデックス番号を求めます。

p = np.argmax(model.predict(X_test), axis=1)
print(p)

[7 2 1 ... 4 5 6]

最後に、テストデータに対して予測したクラスごとに、10個ずつの画像を表示してみます。

fig = plt.figure(figsize=(10, 10))
fig.subplots_adjust(left=0, right=1, bottom=0, top=0.5, hspace=0.1, wspace=-0.9)
for i in range(10):
  k = 0
  for j in range(10):
    while p[k] != i:
      k += 1
    ax = fig.add_subplot(10, 10, i * 10 +  j + 1, xticks=[], yticks=[])
    ax.imshow(X_test[k].reshape((28, 28)), cmap='gray')
    k += 1

参考文献 †

• SequentialモデルでKerasを始めてみよう, Keras Documentation
• Mnist cnn, Keras Documentation
• KerasでDeep Learning：KerasでMNISTデータを扱ってみる, データサイエンティスト(仮)