![[PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png "[PukiWiki]")
はじめに †
ここでは、Rを使って平均、分散、標準偏差を求めます。
『Rによるバイオインフォマティクスデータ解析』の3.3節「基本統計関数」に少しだけ出てきます。
準備 †
Rのインストールについては、次のページを見てください。
ここでは、標準で使用できるirisデータセットを使います。
data(iris)
このデータセットは、アヤメの種類（Species）をがく片の長さ（Sepal.Length）、幅（Sepal.Width）、花びらの長さ（Petal.Length）、幅（Petal.Width）によって分類する問題です。 長さと幅は連続値、種類はsetosa, versicolor, virginicaのいずれかをとる離散値です。
このデータセットには、setosa, versicolor, virginicaという3種類のアヤメについて、それぞれ50個ずつ、合計150個のデータが含まれています。 ランダムに10個のデータを選択して、見てみましょう。
iris[sort(sample(1:150,10)),]
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
論文に使用するグラフはカッコイイ方がいいので、グラフ作成ライブラリーのggplot2でもグラフを作成します。
install.packages("ggplot2") library(ggplot2)
記述統計 †
標本を要約し、標本の情報をわかりやすく記述することを記述統計といいます。
ここでは、散布図、ヒストグラム、ボックスプロット（箱ひげ図）、棒グラフを作成します。
散布図 †
横軸と縦軸にそれぞれ別の量をとり、測定値を点として表したグラフを散布図といいます。 2つの値を同時に測定し、[math]n[/math] 個の測定値の組を [math](x_1, x_2), (x_2, y_2),\dots, (x_n, y_n)[/math] としたとき、それぞれを [math]x[/math] 座標、[math]y[/math] 座標とする点として表したものです。
散布図を作成するには、plot関数を使います。
plot(x=iris$Petal.Length, y=iris$Petal.Width, xlab="Petal.Length", ylab="Petal.Width")
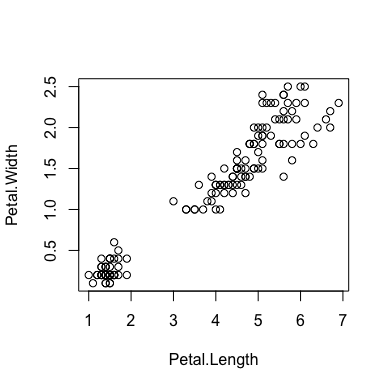
ggplot2で散布図を作成するには、ggplot関数とgeom_point関数を使います。
ggplot(data=iris, aes(x=Petal.Length, y=Petal.Width))+ geom_point()+ theme(aspect.ratio=1)
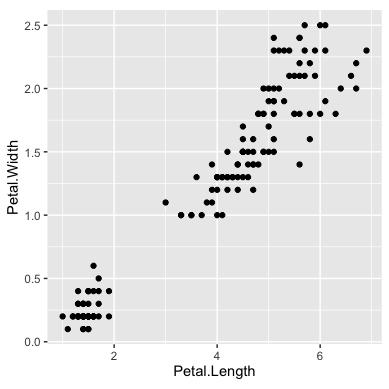
近似直線を追加するには、geom_smooth関数を加えます。
ggplot(data=iris, aes(x=Petal.Length, y=Petal.Width))+ geom_point()+ geom_smooth(method="lm")+ theme(aspect.ratio=1)
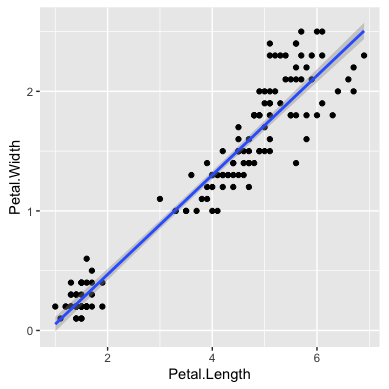
種（Species）ごとに色と形を変えるには、aes関数のcolorとshapeにカテゴリーを表す列を指定します。
ggplot(data=iris, aes(x=Petal.Length, y=Petal.Width, color=Species, shape=Species))+ geom_point()+ theme(aspect.ratio=1)
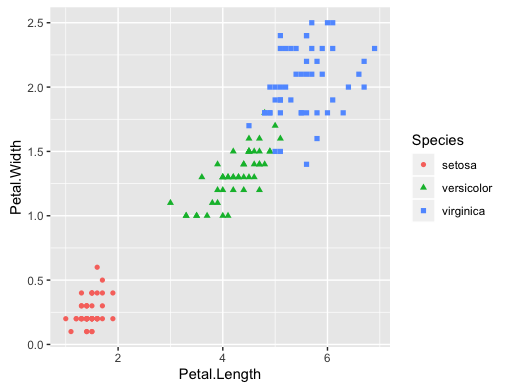
ヒストグラム †
測定値が存在する範囲をいくつかの区間に分け、各区間とその区間に属する測定値の個数との関係性を度数分布と言います。 度数分布を表すグラフをヒストグラムといい、底辺の長さが各区間の幅に比例し、その面積がその区間の度数に比例する長方形を近接して並べたものです。
ヒストグラムを作成するには、hist関数を使います。
versicolor <- iris[51:100,] hist(versicolor$Petal.Length, xlab="Petal.Length", main="")
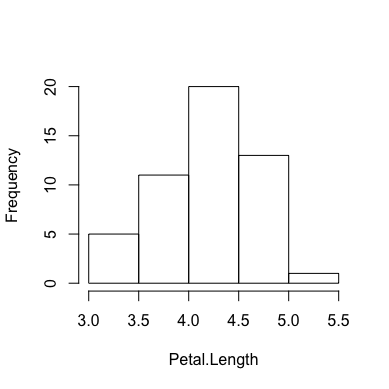
ggplot2でヒストグラムを作成するには、ggplot関数とgeom_histogram関数を使います。
versicolor <- iris[51:100,] ggplot(data=versicolor, aes(x=Petal.Length))+ geom_histogram()+ theme(aspect.ratio=1)
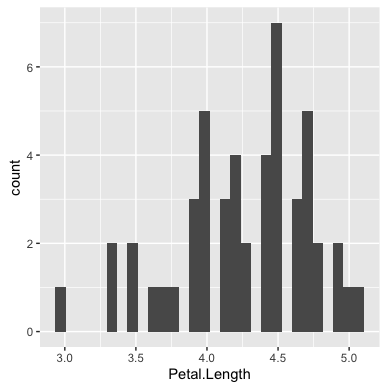
種（Species）ごとに色を変えるには、aes関数のfillにカテゴリーを表す列を指定し、geom_histogram関数のpositionにidentityと指定します。（alphaには透明度を指定します。）
ggplot(data=iris, aes(x=Petal.Length, fill=Species))+ geom_histogram(position="identity", alpha=0.8)+ theme(aspect.ratio=1)
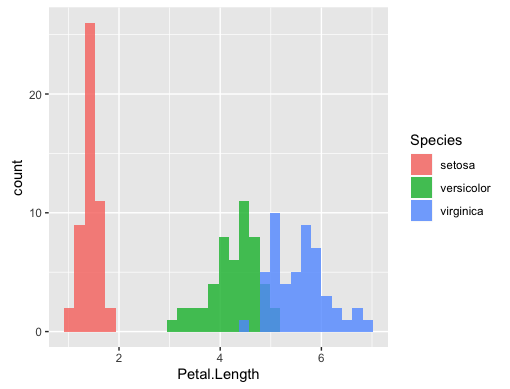
ボックスプロット（箱ひげ図） †
ヒストグラムの他に、測定値の分布やばらつき具合を表すグラフとしてボックスプロット（箱ひげ図）があります。 長方形の箱とその両端から伸びるひげで標本の統計量を表します。
箱の両端は、第一四分位数（最小値から全体の1/4のところにある測定値、25 パーセンタイル）と第三四分位数（最小値から全体の3/4のところにある測定値、75 パーセンタイル）を表し、箱の中の線は中央値（標本の大きさが奇数のときは全体の中央にある測定値、偶数のときは中央の2つの測定値の平均値、メディアン、50% パーセンタイル）を表します。
ひげの表し方には2種類あり、一つはひげの両端が最小値と最大値を表します。 もう一つは、ひげの両端が箱の両端から第三四分位数と第一四分位数の差の1.5倍の範囲内での最小値と最大値を表します。 後者の場合、ひげの両端よりも外側にある測定値を特異値（または外れ値）として丸印で表すこともあります。
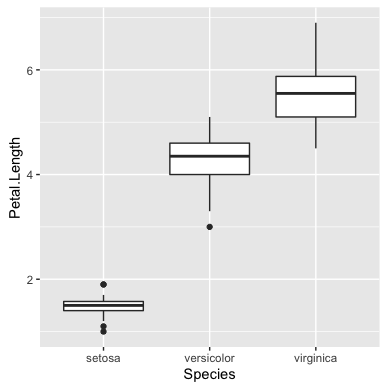
setosa <- iris[1:50,] versicolor <- iris[51:100,] verginica <- iris[101:150,] boxplot(setosa$Petal.Length, versicolor$Petal.Length, virginica$Petal.Length, names=c("Setosa", "Versicolor", "Virginica"), ylab="Petal.Length")
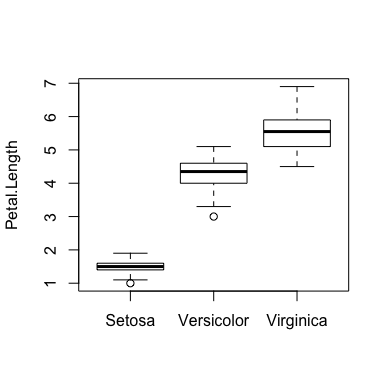
ggplot2でボックスプロットを作成するには、ggplot関数とgeom_boxplot関数を使います。
ggplot(data=iris, aes(x=Species, y=Petal.Length))+ geom_boxplot()+ theme(aspect.ratio=1)
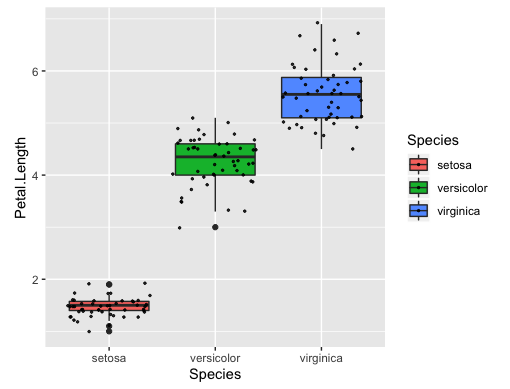
種（Species）ごとに色を変えるには、aes関数のfillにカテゴリーを表す列を指定し、データをプロットするにはgeom_jitter関数を使います。（sizeには点の大きさ、alphaには透明度を指定します。）
ggplot(data=iris, aes(x=Species, y=Petal.Length, fill=Species))+ geom_boxplot()+ geom_jitter(size=0.5, alpha=0.8)+ theme(aspect.ratio=1)
棒グラフ †
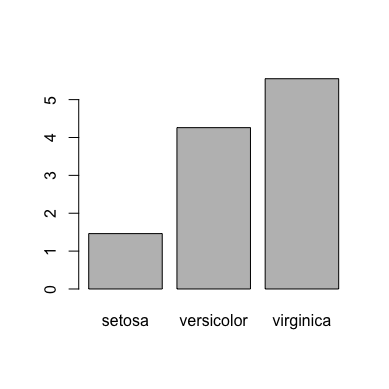
棒グラフを作成するには、barplot関数を使用します。 まずaggregate関数を使って平均を集計し、それを棒グラフにします。
aggr <- aggregate(iris$Petal.Length, by=list(iris$Species), FUN="mean") barplot(aggr$x, names=aggr$Group.1)
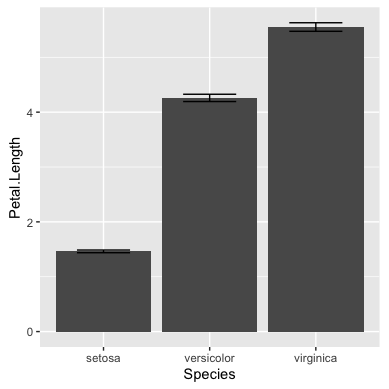
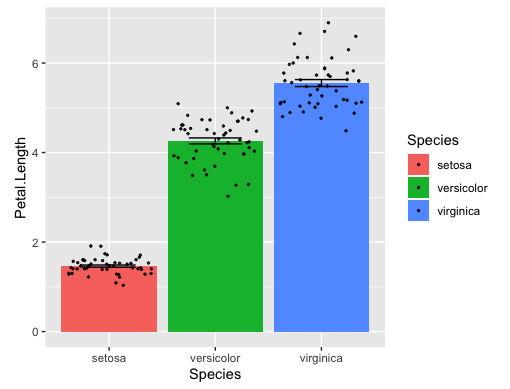
ggplot2で棒グラフを作成するには、ggplot関数とgeom_bar関数を使います。 ここでは、エラーバーを表示するために、stat_summary関数を加えます。
ggplot(data=iris, aes(x=Species, y=Petal.Length))+ geom_bar(stat="summary", fun.y="mean")+ stat_summary(fun.data="mean_se", geom="errorbar", width=0.5)+ theme(aspect.ratio=1)
ボックスプロットと同様に、種（Species）ごとに色を変えるには、aes関数のfillにカテゴリーを表す列を指定し、データをプロットするにはgeom_jitter関数を加えます。（sizeには点の大きさ、alphaには透明度を指定します。）
ggplot(data=iris, aes(x=Species, y=Petal.Length))+ geom_bar(stat="summary", fun.y="mean")+ stat_summary(fun.data="mean_se", geom="errorbar", width=0.5)+ theme(aspect.ratio=1)
推定統計 †
標本から母集団の情報を推定することを推定統計といいます。
平均 †
母平均は、母集団の値の合計を母集団の大きさ [math]N[/math] で割ったものです。 \[ \mu(X) = \frac{1}{N} \sum_{i=1}^N x_i \]
標本平均は、標本の値の合計を標本の大きさ [math]n[/math] で割ったものです。 \[\overline{X} = \frac{1}{n} \sum_{i=1}^{n} x_i \]
標本平均を求めるには、mean関数を使います。
setosa <- iris[1:50,] versicolor <- iris[51:100,] virginica <- iris[101:150,] mean(setosa$Petal.Length) mean(versicolor$Petal.Length) mean(virginica$Petal.Length)
> mean(setosa$Petal.Length) [1] 1.462 > mean(versicolor$Petal.Length) [1] 4.26 > mean(virginica$Petal.Length) [1] 5.552
標本平均の期待値は母平均に等しいため、標本平均を求めることで母平均を推定できます。
分散 †
測定値の標本平均からのズレを偏差といいます。
分散は、値の偏差の二乗の総和を集団の大きさ [math]N[/math] で割ったものです。 \[\sigma(X)^2 = \frac{1}{N} \sum_{i=1}^{n} (x_i - \mu(X))^2 \]
不偏分散（標本不偏分散）は、標本に含まれる値の偏差の二乗の総和を標本数から1を引いた数で割ったものです。 \[ s(X)^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \overline{X})^2 \]
不偏分散を求めるには、var関数を使います。
var(setosa$Petal.Length) var(versicolor$Petal.Length) var(virginica$Petal.Length)
> var(setosa$Petal.Length) [1] 0.03015918 > var(versicolor$Petal.Length) [1] 0.2208163 > var(virginica$Petal.Length) [1] 0.3045878
不偏分散の期待値は母集団の分散に等しいため、不偏分散を求めることで母集団の分散を推定できます。
標準偏差 †
標準偏差は、分散の平方根です。 \[ \sigma(X) = \sqrt{\sigma(X)^2} = \sqrt{\frac{1}{N} \sum_{i=1}^{n} (x_i - \mu(X))^2} \]
不偏標準偏差（標本不偏標準偏差）は、不偏分散の平方根です。 \[ s(X) = \sqrt{s(X)^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \overline{X})} \]
不偏標準偏差を求めるには、sd関数を使います。
sd(setosa$Petal.Length) sd(versicolor$Petal.Length) sd(virginica$Petal.Length)
> sd(setosa$Petal.Length) [1] 0.173664 > sd(versicolor$Petal.Length) [1] 0.469911 > sd(virginica$Petal.Length) [1] 0.5518947
不偏標準偏差の期待値は母集団の標準偏差に等しいため、不偏標準偏差を求めることで母集団の標準偏差を推定できます。
不確かさ †
「平均 [math]\mu(X)[/math]、標準偏差 [math]\sigma(X)[/math] の母集団から無作為に抽出した大きさ [math]n[/math] の標本の平均 [math]\overline{X}[/math] は、平均 [math]\mu(X)[/math]、標準偏差 [math]\frac{\sigma(X)}{\sqrt{n}}[/math] の正規分布に従う」という中心極限定理より、[math]n[/math] 個の測定値を平均すると標準偏差が [math]\frac{1}{\sqrt{n}}[/math] になることがわかります。
不偏標準偏差 [math]s(X)[/math] を標本の大きさの平方根 [math]\sqrt{n}[/math] で割ったものを、標準不確かさ（標準誤差）といいます。 \[ u(X) = \frac{s(X)}{\sqrt{n}} \]
標準不確かさに包含係数 [math]k[/math] をかけたものを拡張不確かさといいます。 \[ U(X) = k \times u(X) \]
測定値が正規分布に従っていて、測定値が11個以上あるとき、測定値の95%が包含係数 [math]k=2[/math] の [math]\overline{X} \pm U(X)[/math] の範囲に含まれます。 この95%のことを信頼水準といいます。
1993年にISOを含む7つの国際機関が策定した「計測における不確かさの表現ガイド」に従うと、測定値は標準不確かさまたは拡張不確かさを用いて、次のように表します。
- [math]x = \overline{X}[/math]、標準不確かさは [math]u(X)[/math]
- [math]x = (\overline{X} \pm U(X))[/math]、ただし記号 [math]\pm[/math] に続く値は包含係数 [math]k=2[/math] から決定された拡張不確かさである
標準不確かさを求めるには、標本標準偏差を求めるsd関数と平方根を求めるsqrt関数を使います。
sd(setosa$Petal.Length) / sqrt(50) sd(versicolor$Petal.Length) / sqrt(50) sd(virginica$Petal.Length) / sqrt(50)
> sd(setosa$Petal.Length) / sqrt(50) [1] 0.0245598 > sd(versicolor$Petal.Length) / sqrt(50) [1] 0.06645545 > sd(virginica$Petal.Length) / sqrt(50) [1] 0.0780497
これを用いて、SetosaのPetal.Lengthの測定値を「長さ [math]l = 1.462[/math] cm、標準不確かさは [math]0.025[/math] cm」または「長さ [math]l = (1.462 \pm 0.049)[/math] cm、ただし記号 [math]\pm[/math] に続く値は包含係数 [math]k=2[/math] から決定された拡張不確かさである」と表します。
95%信頼区間 †
計測における不確かさの表し方が分野によってバラバラなのは良くないので「計測における不確かさの表現ガイド」が作成されましたが、 95%信頼区間もまだよく使われています。
95%信頼区間は、母集団の平均が95%の確率で含まれると推定される区間のことです。
標本の平均と母集団の平均の偏差を標準不確かさで割ったものをt値（t統計量）といいます。 \[ t(X) = \frac{\overline{X} - \mu(X)}{u(X)} \]
t値は、自由度 [math]n - 1[/math] のt分布（自由度が大きいほど正規分布に近づく分布）に従うことがわかっています。 そこで、この分布において上側の面積の割合が2.5%になるt値 [math]t_{n-1,2.5\%}[/math] を求め、これに標準不確かさ [math]u(X)[/math] を掛けると95%信頼区間の幅の半分が求まります。 つまり、母平均の95%信頼区間は次のように表されます。 \[ \overline{X} - t_{n-1,2.5\%} \times u(X) \le \mu \le \overline{X} + t_{n-1,2.5\%} \times u(X) \]
計測の不確かさを表すのに95%信頼区間を用いるとき、測定値は次のように表します。
- [math]\overline{X}[/math]（95%信頼区間 [math]\overline{X} - t_{n-1,2.5\%} \times u(X)[/math]–[math]\overline{X} + t_{n-1,2.5\%} \times u(X)[/math]）
95%信頼区間を求めるには、t.test関数を使います。
t.test(setosa$Petal.Length)
> t.test(setosa$Petal.Length) One Sample t-test data: setosa$Petal.Length t = 59.528, df = 49, p-value < 2.2e-16 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: 1.412645 1.511355 sample estimates: mean of x 1.462
95%信頼区間 (95 percent confidence interval) のところを見ると、SetosaのPetal.Lengthの母平均の95%信頼区間は [math][1.412645, 1.511355][/math] です。
そこで、SetosaのPetal.Lengthの測定値を「長さは [math]1.462[/math] cm（95%信頼区間 [math]1.412[/math]–[math]1.511[/math] cm）だった」と表します。
演習 †
Sepal.LengthとSepal.Widthの関係を表す散布図、VersicolorのSepal.Lengthの分布を表すヒストグラム、SetosaとVersicolorとVirginicaのSepal.Lengthの分布を表すボックスプロットを作成しよう。
Setosa, Versicolor, VirginicaのSepal.Lengthについて、それぞれの標本平均 [math]\overline{X}[/math] と標本標準偏差 [math]s(X)[/math] を求めてみよう。
参考文献 †
- 樋口千洋: Rによるバイオインフォマティクスデータ解析 第2版－Bioconductorを用いたゲノムスケールのデータマイニング－, 共立出版 (2011)
ggplot2_scatter_bw_lm.png
ggplot2_bar.png
ggplot2_bar_bw.png
barplot.png
scatter.png
histogram.png
boxplot.png
ggplot2_boxplot.png
ggplot2_boxplot_bw.png
ggplot2_histogram.png
ggplot2_histogram_bw.png
ggplot2_scatter.png
ggplot2_scatter_bw.png
