はじめに †
ロジスティック回帰は、教師信号 [math]y[/math] が 1 または 0 の2値分類問題(カテゴリーが「はい」と「いいえ」のカテゴリー分析)において、[math]y = 1[/math] となる確率を表す関数を回帰分析によって求める手法です。
『Rによるバイオインフォマティクスデータ解析』には載っていません。
準備 †
Rのインストールについては,次のページを見てください.
ここでは、標準で使用できるirisデータセットを使います。
data(iris)
このデータセットは、アヤメの種類(Species)をがく片の長さ(Sepal.Length)、幅(Lepal.Width)、花びらの長さ(Petal.Length)、幅(Petal.Width)によって分類する問題です。 長さと幅は連続値,種類はsetosa, versicolor, virginicaのいずれかをとる離散値です。
このデータセットには、setosa, versicolor, virginicaという3種類のアヤメについて、それぞれ50個ずつ、合計150個のデータが含まれています。 ランダムに10個のデータを選択して、見てみましょう。
iris[sort(sample(1:150,10)),]
Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
2値分類にするため、Speciesがsetosaなら 1、そうでないなら 0 という新しい列 Setosa を作ります。 これを、versicolor, virginica についても行います。
iris$Setosa <- ifelse(iris$Species=="setosa", 1, 0) iris$Versicolor <- ifelse(iris$Species=="versicolor", 1, 0) iris$Virginica <- ifelse(iris$Species=="virginica", 1, 0)
もう一度、ランダムに10個のデータを選択して、追加した列を確認します。
Sepal.Length Sepal.Width Petal.Length Petal.Width Species Setosa Versicolor Virginica 21 5.4 3.4 1.7 0.2 setosa 1 0 0 43 4.4 3.2 1.3 0.2 setosa 1 0 0 50 5.0 3.3 1.4 0.2 setosa 1 0 0 54 5.5 2.3 4.0 1.3 versicolor 0 1 0 73 6.3 2.5 4.9 1.5 versicolor 0 1 0 76 6.6 3.0 4.4 1.4 versicolor 0 1 0 84 6.0 2.7 5.1 1.6 versicolor 0 1 0 114 5.7 2.5 5.0 2.0 virginica 0 0 1 139 6.0 3.0 4.8 1.8 virginica 0 0 1 150 5.9 3.0 5.1 1.8 virginica 0 0 1
これをランダム・サンプリングして80%を訓練データとし、のこりの20%をテスト・データとします。
idx <- sample(nrow(iris), as.integer(nrow(iris)*0.8)) iris.train <- iris[idx,] iris.test <- iris[-idx,]
ロジスティック回帰 †
説明のため、まずは説明変数をPetal.Length、目的変数をVirginicaとします。
x.train <- iris.train$Petal.Length y.train <- iris.train$Virginica plot(x.train, y.train)
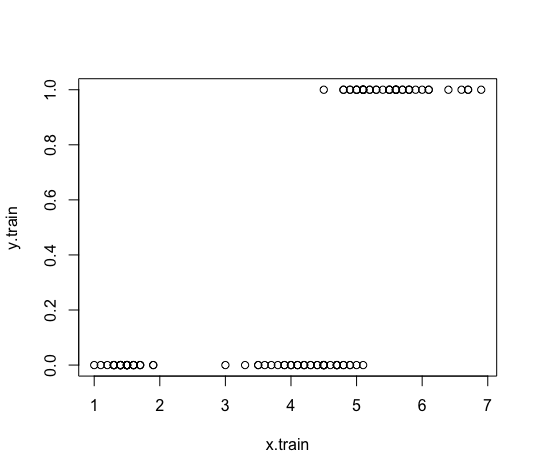
このデータに対して線形回帰でモデルを作成すると、うまくフィットしません。
model <- lm(y.train ~ x.train) abline(model)
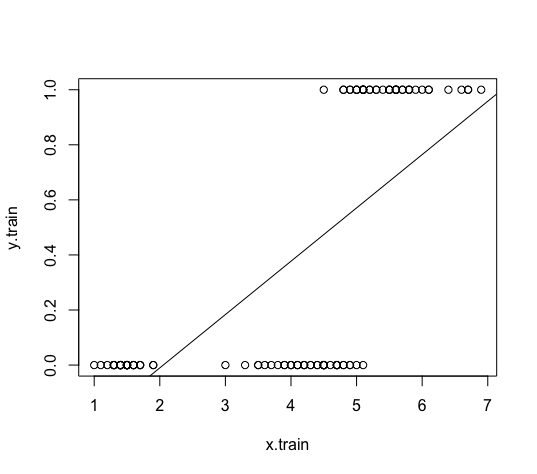
そこで、目的変数の値が 1 になる確率を [math]p[/math] とし、この確率を $$ p = \frac{1}{1+\exp(-(\beta_0+\beta_1 x))} $$ という関数で近似することを考えます。
この関数は、次のような 0 から 1 までの値をとり、S字の形をしています。
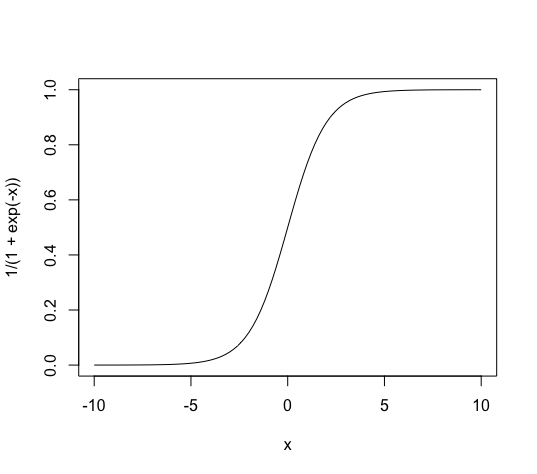
この式を変形すると、次のようになります。 $$ \log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 x$$ 左辺の [math]\frac{p}{1-p}[/math] をオッズ (odds) といい、[math]\log\left(\frac{p}{1-p}\right)[/math] をロジット関数といいます。
このロジット関数を線形回帰で求めるのがロジスティック回帰です。
ロジスティック回帰を実行する †
ロジスティック回帰を行うには、glm関数を使います。 glm関数には、第1引数にモデル式、第2引数にデータフレーム、第3引数に family=binomial(link="logit") を指定します。
model <- glm(Virginica ~ Petal.Length, data=iris.train, family=binomial(link="logit"))
学習したモデルのサマリーを出力してみます。
summary(model)
Call: glm(formula = Virginica ~ Petal.Length, family = binomial(link = "logit"), data = iris.train) Deviance Residuals: Min 1Q Median 3Q Max -2.02963 -0.03626 0.00000 0.02848 2.51612 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -40.965 11.058 -3.705 0.000212 *** Petal.Length 8.409 2.267 3.709 0.000208 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 154.11 on 119 degrees of freedom Residual deviance: 31.59 on 118 degrees of freedom AIC: 35.59 Number of Fisher Scoring iterations: 9
CoefficientsのEstimateがロジスティック回帰で求められたロジット関数の係数を表しており、Interceptが定数項 [math]\beta_0[/math] です。 したがって、目的変数の値が 1 になる確率は次のように表されます。 $$ p = \frac{1}{1 + \exp(-(-40.965 + 8.409 x))} $$
これをプロットしてみます。
plot(x.train, y.train) curve(1/(1+exp(-(-40.965+8.409*x))), add=TRUE)
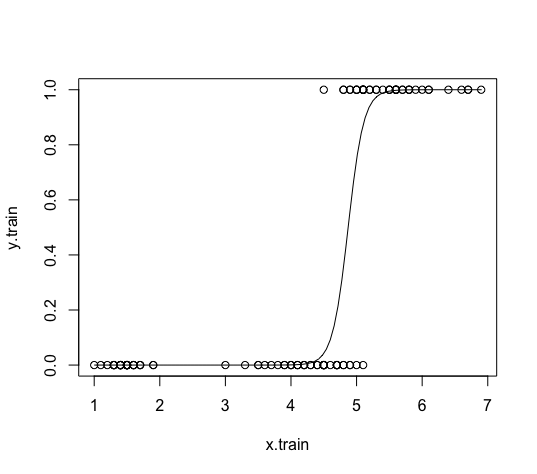
訓練データに対する確率は、fitted関数で出力できます。
fitted(model)
26 85 58 100 86 105 48 66 135 129 90 1.129131e-12 4.219567e-02 1.825599e-06 1.522187e-03 4.219567e-02 9.995945e-01 2.100456e-13 1.864666e-02 9.978238e-01 9.978238e-01 6.570957e-04 118 11 67 19 127 2 84 102 130 68 41 9.999998e-01 4.870000e-13 4.219567e-02 2.617940e-12 3.544564e-01 2.100456e-13 8.725072e-01 8.725072e-01 9.995945e-01 1.522187e-03 2.220446e-16...
インデックスをランダムに選んだままでソートしていないので、順番はバラバラになっています。
テストデータに対して予測をするときは、predict.glm関数を用います。 predict.glm関数の第1引数には学習したモデル、第2引数にはテストデータのデータフレーム、第3引数にはtype="response"を指定します。
predict.glm(model, iris.test, type="response")
5 7 18 22 24 30 33 36 38 39 43 2.100456e-13 2.100456e-13 2.100456e-13 4.870000e-13 2.617940e-12 1.129131e-12 4.870000e-13 2.220446e-16 2.100456e-13 2.220446e-16 2.220446e-16 47 55 59 62 70 72 76 91 93 94 103 1.129131e-12 9.267631e-02 9.267631e-02 3.522188e-03 2.835147e-04 6.570957e-04 1.864666e-02 1.864666e-02 6.570957e-04 1.825599e-06 9.998250e-01 108 115 124 126 131 141 145 149 9.999939e-01 8.725072e-01 5.600666e-01 9.999245e-01 9.999675e-01 9.978238e-01 9.990602e-01 9.884120e-01
モデルの評価 †
ロジスティック回帰で求めたモデルを評価するには、ROC曲線の下側の面積 (AUC: Area Under the Curve) を使います。
ROC曲線とAUCを求めるにはpROCパッケージを使います。
install.packages("pROC") library(pROC)
テストデータの目的変数とテストデータに対する予測値を変数に代入しておき、roc関数でROC曲線とAUCを求めます。
y.test <- iris.test$Virginica p.test <- predict.glm(model, iris.test, type="response") roc(y.test, p.test)
Call: roc.default(response = y.test, predictor = p.test) Data: p.test in 19 controls (y.test 0) < 11 cases (y.test 1). Area under the curve: 0.9928
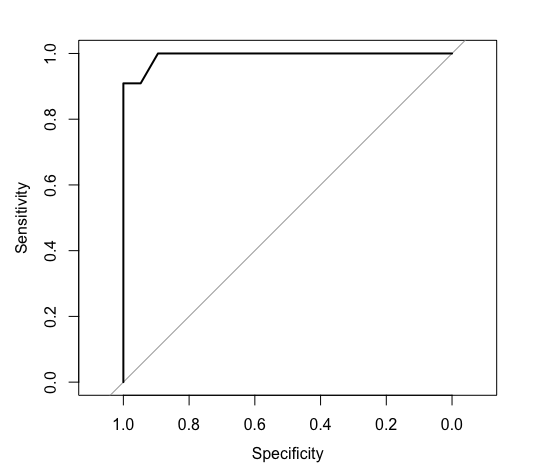
ROC曲線をプロットするには、roc関数で生成されるオブジェクトをplot関数に渡します。
roc <- roc(y.test, p.test) plot(roc)
まとめ †
ロジスティック回帰は、目的変数が 1 になる確率のロジット関数を線形回帰によって求める手法で、2値分類(カテゴリーが「はい」または「いいえ」のカテゴリー分析)に用いる手法です。
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)