- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rで主成分分析する へ行く。
はじめに †
ここでは,Rを使って主成分分析を行います.
『Rによるバイオインフォマティクスデータ解析』にも載っていますが,あまり参考にはしていません.
準備 †
Rのインストールについては,次のページを見てください.
主成分分析 †
主成分分析 (Principal Component Analysis, PCA) は,多変量解析の一手法で,高次元の数値データに対して合成成分を作る手法です.
この合成成分のことを主成分といい,次のように表されます. \[ \begin{array}{c@{}c@{}c} z_1 &=& a_{1,1} x_{1} + a_{1,2} x_{2} + \dots + a_{1,p} x_{p} \\ z_2 &=& a_{2,1} x_{1} + a_{2,2} x_{2} + \dots + a_{2,p} x_{p} \\ \vdots & & \\ z_p &=& a_{p,1} x_{1} + a_{p,2} x_{2} + \dots + a_{p,p} x_{p} \end{array} \] ここで,[math]z_1[/math] を第1主成分,[math]z_2[/math] を第2主成分,つまり,[math]z_i[/math] を第 [math]i[/math] 主成分といいます.
次元数が [math]p[/math] のとき,主成分は [math]p[/math] 個できます. このうちの第1主成分からいくつかだけを使ってデータを表現できないかということを考えます.
例として,次のような2次元のデータを考えてみます*1.
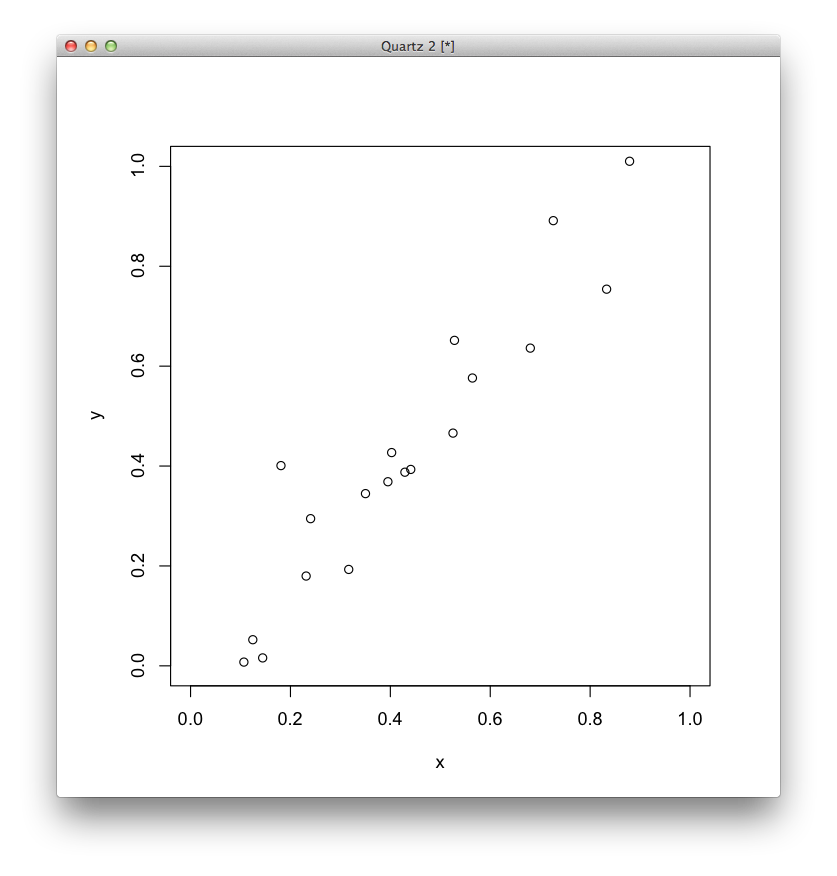
2次元の場合,主成分(合成成分)は次のようになります. (図では変数が [math]x[/math], [math]y[/math] になっていますが,これを [math]x_1[/math], [math]x_2[/math]とします.) \[ \begin{array}{c@{}c@{}c} z_1 &=& a_{1,1} x_{1} + a_{1,2} x_{2} \\ z_2 &=& a_{2,1} x_{1} + a_{2,2} x_{2} \end{array} \]
このデータは2変数で表現されていますが,これを第1主成分だけで表現するとしたら,どのように第1主成分を選ぶ,つまり,どのように第1主成分の係数 [math]a_{1,1}[/math], [math]a_{1,2}[/math] を選ぶのがいいのかを考えます.
合成成分である第1主成分だけでデータを表現するということは,データを1次元で表現するということですから,データから第1主成分を表す直線に垂線を下ろし,その値でデータを表現するということになります.
下の図のように,データから第1主成分である直線に垂線を下ろしたときに同じような場所になってしまう,つまり,分散が小さいのはよくありません.
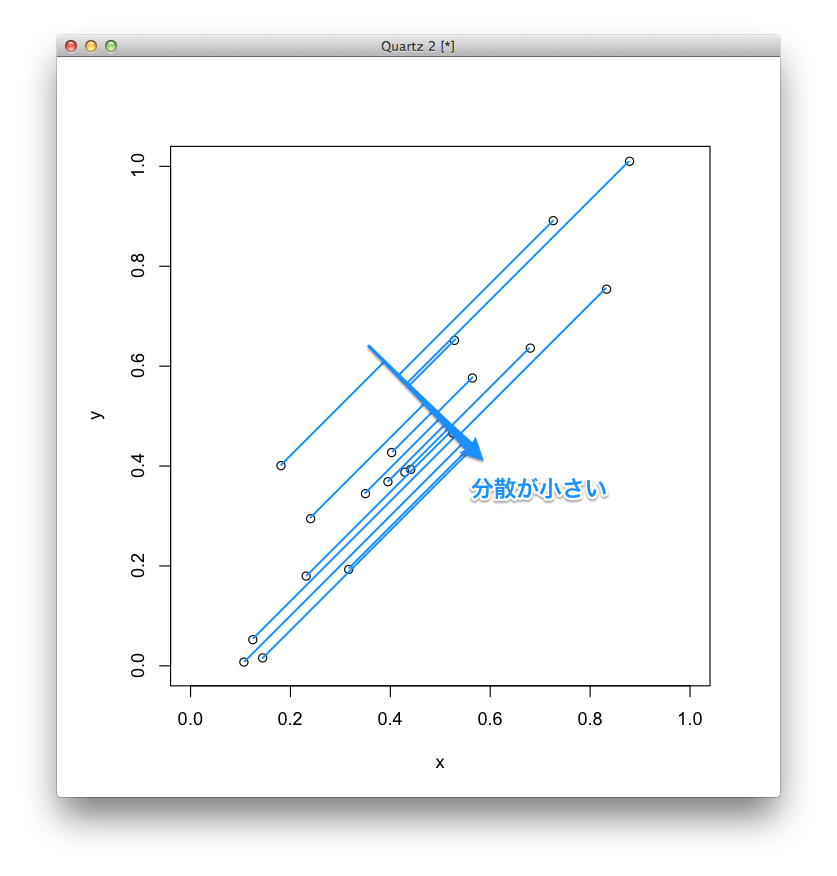
逆に,下の図のように,データから第1主成分である直線に垂線を下ろしたときにバラツキが大きくなる,つまり,分散が大きくなるほうが,データを良く表していると考えます.
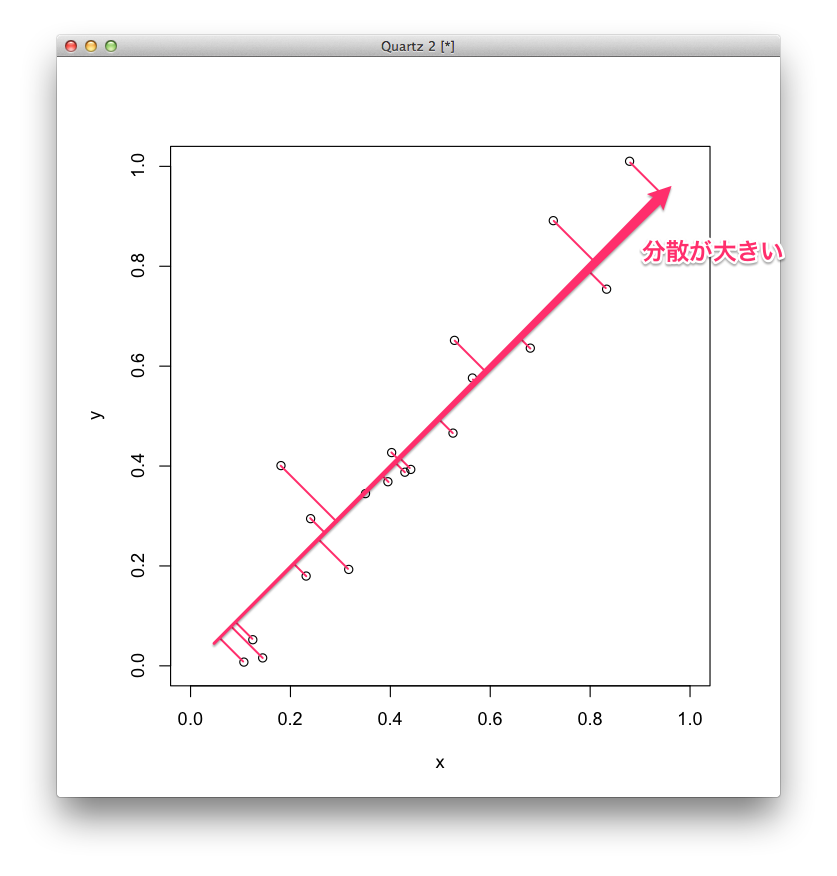
そこで,垂線を下ろしたときに分散が最も大きくなる直線を第1主成分とします.
第2主成分は,第1主成分と直行する直線の中で,データから垂線を下ろしたときに分散が最も大きくなる直線とし,以後同様に,第 [math]i+1[/math] 成分は第 [math]i[/math] 主成分と直行する直線の中で,データから垂線を下ろしたときに分散が最も大きくなる直線とします. 最後の主成分である第 [math]p[/math] 主成分は,選ぶことができずに決まります.
今回の例は2次元なので,第2主成分は第1主成分に直行する直線に決まってしまい,下の図のようになります.
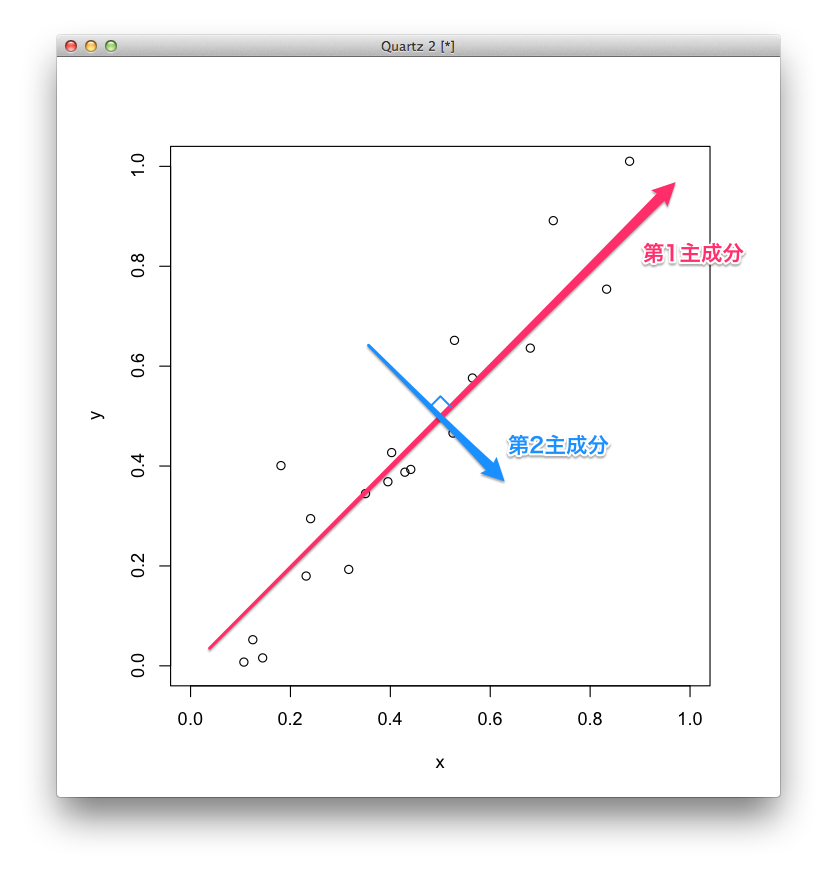
主成分を求めるには,まず各変数を平均0,標準偏差1に正規化(標準化)し,分散共分散行列の固有値と固有ベクトルを求めます.
分散共分散行列とは、行列の [math]i[/math] 行 [math]j[/math] の要素が、[math]i[/math] 次元目の値と [math]j[/math] 次元目の値の共分散 [math]Cov(X_i,X_j)[/math] になっている行列です。 対角要素は分散になるので、分散共分散行列と呼ばれます。
分散共分散行列は [math]p \times p[/math] 正方行列なので,固有値は [math]p[/math] 個求まります. これを大きい順に [math]\lambda_1[/math], [math]\lambda_2[/math], [math]\dots[/math], [math]\lambda_p[/math] と並べます. このとき,[math]i[/math] 番目の固有値 [math]\lambda_i[/math] に対応する固有ベクトルが第 [math]i[/math] 主成分になります. 固有ベクトルは,その主成分と元の変数との相関係数を表しています. 固有値は,その主成分の分散を表しています.
上の図の例では,最も大きい固有値が約1.96で,それに対応する固有ベクトルが約 [math]\left(\begin{array}{r}0.707 \\ 0.707 \end{array} \right)[/math],その次に大きい固有値が約0.04で,それに対応する固有ベクトルが約 [math]\left( \begin{array}{r} -0.707 \\ 0.707 \end{array}\right)[/math]となります. したがって,第1主成分が約 [math]\left(\begin{array}{r}0.707 \\ 0.707 \end{array} \right)[/math] で,その分散が約1.96,第2主成分が約 [math]\left( \begin{array}{r} -0.707 \\ 0.707 \end{array}\right)[/math] で,その分散が約0.04となります. 第1主成分は,[math]x_1[/math], [math]x_2[/math] との相関係数が約0.707です. 第2主成分は,[math]x_1[/math] との相関係数が約-0.707,[math]x_2[/math] との相関係数が約0.707です.
データを正規化して,第 [math]i[/math] 主成分に垂線を下ろしたところの値を第 [math]i[/math] 主成分の主成分スコアといいます.
図の一番左下のデータは,約 (0.107, 0.008) です. [math]x_1[/math] の平均は約0.46,標準偏差は約0.27ですから,[math]x_1[/math] を正規化すると(0.107 - 0.46) / 0.27 = -1.29となります. [math]x_2[/math] の平均は約0.47,標準偏差は約0.33ですから,[math]x_2[/math] を正規化すると(0.008 - 0.47) / 0.33 = -1.38になります.
おおよそ (-1.29, -1.38) から第1主成分と第2主成分に垂線を下ろしたところの値が,それぞれの主成分スコアとなりますが,これは,正規化された値に固有ベクトルを掛けて求めることができます. 第1主成分の主成分スコアは,0.707 * -1.29 + 0.707 * -1.38 = -1.89となり,第2主成分の主成分スコアは,-0.707 * -1.29 + 0.707 * -1.38 = -0.06となります.
ある固有値を固有値全部の合計で割った値を主成分寄与率といいます. つまり,第 [math]i[/math] 主成分の寄与率は以下の式で表されます. \[ \frac{\lambda_i}{\sum_{j=1}^{p} \lambda_{j}} \] 固有値は分散を表していますから,寄与率は主成分全体の分散のうちその主成分の分散の割合を表しています.
また,主成分全体の分散のうち第1主成分から第 [math]i[/math] 主成分までの分散の和の割合を累積寄与率といい,以下の式で表されます. \[ \frac{\sum_{j=1}^{i} \lambda_j}{\sum_{j=1}^{p} \lambda_{j}} \] この累積寄与率が0.8あればいいとか,0.9あればいいというように決めて,どこまでの主成分を採用するかを決めます.
上の例では,第1主成分の分散は約1.96,第2主成分の分散は0.04です. したがって,第1主成分の寄与率は約0.98,第2主成分の寄与率は0.02です. また,累積寄与率は,第1主成分までで約0.98,第2主成分までで1となります.
ここで,累積寄与率が0.9まででいいとするなら,第2主成分は採用せずに第1主成分だけでデータを表現してもいいことになります. 当然のことですが,情報量は落ちるので注意が必要です.
主成分分析を行う †
標準で使えるirisデータセットに対して,主成分分析を行ってみましょう.
> data(iris)
このデータセットは,アヤメの種類(Species)をがく片の長さ(Sepal.Length),幅(Sepal.Width),花びらの長さ(Petal.Length),幅(Petal.Width)によって分類する問題です. 長さと幅は連続値,種類はsetosa, versicolor, virginicaのいずれかをとる離散値です.
このデータセットには,setosa, versicolor, virginicaという3種類のアヤメについて,それぞれ50個ずつ,合計150個のデータが含まれています. ランダムに10個のデータを選択して,見てみましょう.
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
Rで主成分分析を行うには,princomp関数を使います. ただし,princomp関数はデータ数が次元数 [math]p[/math] より小さいときは使えません. そのときは,princomp関数の代わりにprcomp関数を使います*2. princomp関数の第1引数にはモデル式を与え,オプションとして使用するデータをdataオプションで,正規化を行うことをcorオプションで指定します.
> model <- princomp(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width, data=iris, cor=T)
モデル式は「目的変数 ~ 説明変数1 + 説明変数2 + ...」という形ですが,主成分分析には目的変数がないため,目的変数を指定せずに説明変数だけをモデル式に指定します.
主成分分析の結果を表示してみると,次のようになります.
> model Call: princomp(formula = ~Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, data = iris, cor = T) Standard deviations: Comp.1 Comp.2 Comp.3 Comp.4 1.7083611 0.9560494 0.3830886 0.1439265 4 variables and 150 observations. > summary(model) Importance of components: Comp.1 Comp.2 Comp.3 Comp.4 Standard deviation 1.7083611 0.9560494 0.38308860 0.143926497 Proportion of Variance 0.7296245 0.2285076 0.03668922 0.005178709 Cumulative Proportion 0.7296245 0.9581321 0.99482129 1.000000000
summary関数の結果には,各主成分の標準偏差 (Standard deviation),寄与率 (Proportion of Variance),累積寄与率 (Cumulative Proportion) が表示されています.
第2主成分 (Comp. 2) までで累積寄与率が約0.96ありますから,採用するのは第2主成分までで良さそうです.
作成されたオブジェクトのloadings変数に固有ベクトルが格納されています. unclass関数を用いて,固有ベクトル行列だけを取り出します.
> unclass(model$loadings) Comp.1 Comp.2 Comp.3 Comp.4 Sepal.Length 0.5210659 -0.37741762 0.7195664 0.2612863 Sepal.Width -0.2693474 -0.92329566 -0.2443818 -0.1235096 Petal.Length 0.5804131 -0.02449161 -0.1421264 -0.8014492 Petal.Width 0.5648565 -0.06694199 -0.6342727 0.5235971
第1主成分はSepal.Length, Petal.Length, Petal.Widthを同じ程度合成し,これらが大きくなると第1主成分の値も大きくなります. また,Sepal.Widthは他の変数に比べると半分くらいしか影響せず,Sepal.Widthが小さくなると第1主成分の値が大きくなります. したがって,第1主成分は,主に萼(がく)片の長さ,花びらの長さ,幅の大きさと萼(がく)片の幅の小ささを表していると言えます.
第2主成分は,Sepal.Widthと強い負の相関があり,Sepal.Lengthとやや強い負の相関があります. したがって,第2主成分は,萼(がく)片の小ささを表していると言えます.
固有値あるいは各主成分の分散を求めるには,標準偏差を2乗します. 標準偏差は,作成されたオブジェクトのsd変数またはsdev変数に格納されています.
> model$sd^2 Comp.1 Comp.2 Comp.3 Comp.4 2.91849782 0.91403047 0.14675688 0.02071484
各データの主成分スコアは,作成されたオブジェクトのscores変数に格納されています.
> model$scores Comp.1 Comp.2 Comp.3 Comp.4 1 -2.26470281 -0.480026597 0.127706022 0.024168204 2 -2.08096115 0.674133557 0.234608854 0.103006775 3 -2.36422905 0.341908024 -0.044201485 0.028377053 4 -2.29938422 0.597394508 -0.091290106 -0.065955560 5 -2.38984217 -0.646835383 -0.015738196 -0.035922813 ...
主成分分析の結果を第1主成分と第2主成分だけで表示するには,biplot関数を使います.
> biplot(model)
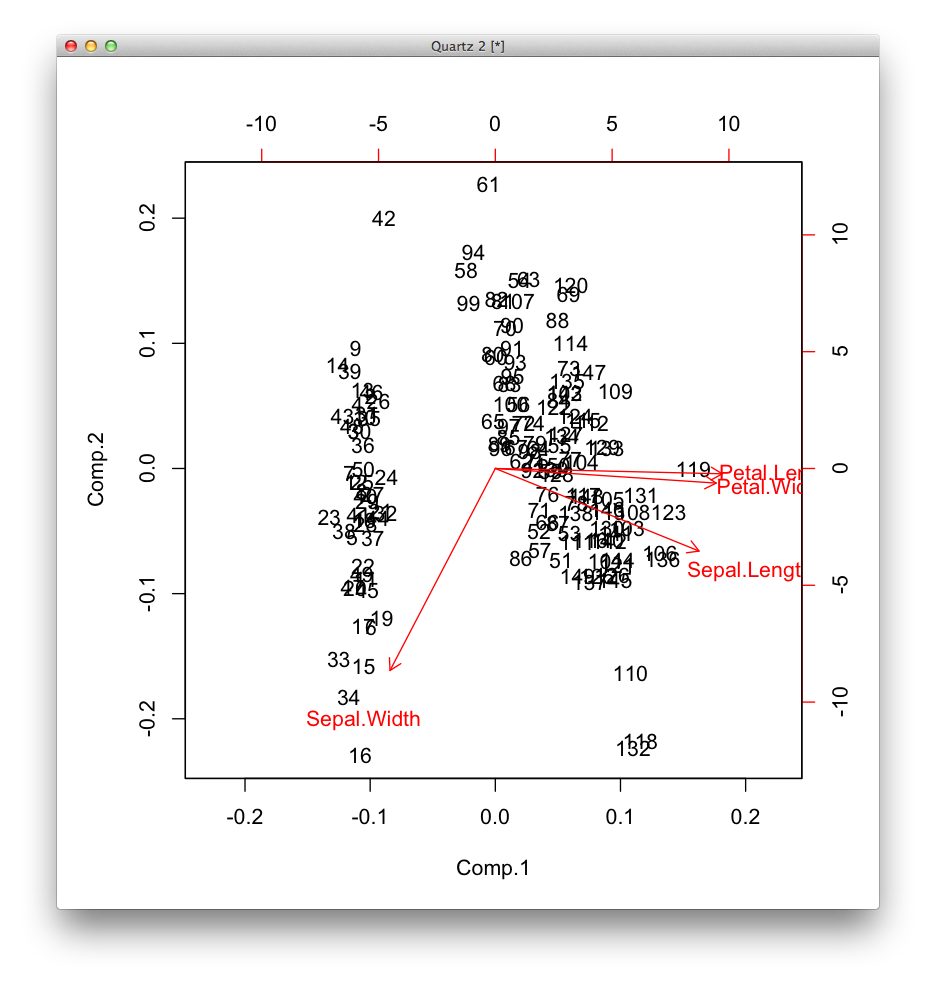
データは正規化されているので,中心は原点になっています. 赤い矢印は,固有ベクトルにおける各変数の値を上軸と右軸で表しています.
まとめ †
主成分分析は,分散が大きい合成成分を求めることによって,変数の数を減らします.
主成分分析では,各次元の値がそれぞれ正規分布になっていることを仮定し,分散が大きなものを重要な主成分とします. したがって,正規分布でないときにはうまくいきません. そういうときは,独立成分分析 (ICA) がうまくいくかもしれません.
演習 †
irisデータを使って、自分で主成分分析をやってみよう。
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)