機械学習/Pythonで学習パラメーターを最適化する のバックアップ(No.7)

目次 †

↑

はじめに †

前回、Pythonの機械学習ライブラリーscikit-learnを用いて、決定木による分類を行いました。

前回はすべての訓練データを使って予測モデルを学習しましたが、実際のデータに対する分析では、訓練データから予測モデルを学習して、テストデータに対して予測をして終わり、ということにはなりません。

例えば、機械学習の手法を決定木に限定した場合でも、木の深さは3でいいのか、4がいいのか、それとも2でもいいのか、評価基準はジニ係数と情報量利得のどちらがいいのかなど、複数の学習パラメーターのうち、どれがいいのか検討しなければなりません。

ここでは、学習した予測モデルの評価と学習パラメーターの最適化について説明します。

環境やデータは前回と同じです。

↑

学習した予測モデルの評価 †

前回は、訓練データから学習した予測モデルのスコア（ここでは、平均正解率）を、訓練データを用いて求めました。

clf.fit(X, y)
clf.score(X, y)

実際の分析では、予測する対象は訓練データ以外のデータであるため、いくら訓練データに対して優れた予測モデルが学習できたとしても、それ以外のデータに対してうまく予測ができないと意味がありません。

そこで、訓練データを全て学習に使わずに、学習用データと検証用データに分割し、学習用データから学習した予測モデルのスコアを検証用データを用いて求めます。

sklearn.model_selectionのtrain_test_splitを用いて、訓練データを学習用データと検証用データに分割します。

from sklearn.model_selection import train_test_split
X_train, X_valid, y_train, y_valid = \
  train_test_split(X, y, test_size=0.2, random_state=0)

ここでは、検証用データのサイズ (test_size) を20% (0.2) としています。 random_stateは、乱数生成器のシードを表します。

次のようにすると、学習用データと検証用データに分割されたことを確認できます。

print(X_train.shape)
print(X_valid.shape)

fit関数を用いて学習用データから学習し、score関数を用いて検証用データに基づいて評価します。

clf.fit(X_train, y_train)
clf.score(X_valid, y_valid)

学習した予測モデルは、学習用データに対するスコアは 1.0 ですが、検証用データに対するスコアは 0.867 となりました。 つまり、実際の平均正解率は86.7%程度であると見込まれます。

今回学習された予測モデルはこちら（前回の続きなので、criterion が entropy、max_depth が 3 です）。 nolink

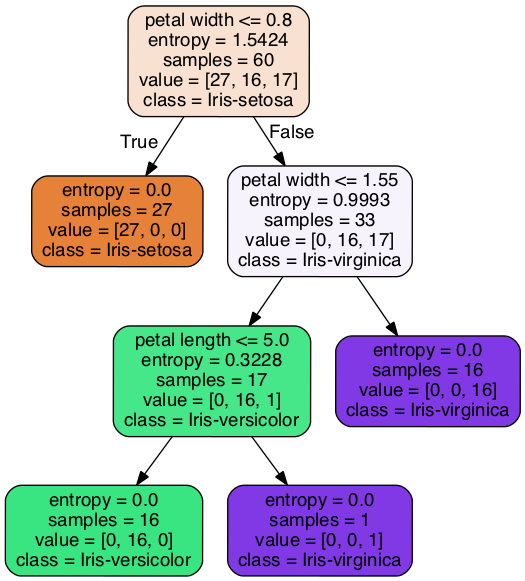
このように、どの学習パラメーターを用いるのが良いかについては、検証用データに対するスコアで評価しないといけません。

↑

クロス・バリデーション †

上の評価では、sklearn.model_selectionクラスのtrain_test_split関数を用いて、訓練データをランダムに学習用データと検証用データに分割しました。

乱数を使っているため、偶然に、予測が難しいデータばかりが検証用データに分けられると、スコアが悪くなってしまいます。

そこで、何回か学習とスコアの計算を行い、その平均を求めます。

↑

[math]k[/math]-フォールド・クロス・バリデーション †

[math]k[/math]-フォールド・クロス・バリデーション ([math]k[/math]-fold Cross Validation) は、訓練データを [math]k[/math] 等分し、[math]i[/math] 番目のグループを検証用データ、それ以外を学習用データとして学習とスコアの計算を行うことを、[math]i = 1[/math] から [math]k[/math] まで、 [math]k[/math] 回繰り返す評価方法です。

[math]k[/math]-フォールド・クロス・バリデーションを行うには、sklearn.model_selectionクラスのcross_val_score関数を用いて、cvオプションに分割数 [math]k[/math] を指定し、結果のスコア配列の平均を求めます。

from sklearn.model_selection import cross_val_score
scores = cross_val_score(clf, X, y, cv=5)
scores.mean()

ファイブ・フォールド・クロス・バリデーションを行なったところ、平均正解率は97.2%でした。

↑

リーブ・ワン・アウト・クロス・バリデーション †

リーブ・ワン・アウト・クロス・バリデーション (Leave One Out Cross Validation) は、[math]i[/math] 番目のデータだけを検証用データ、それ以外を学習用データとして学習とスコアの計算を行うことを、[math]i = 1[/math] からデータの個数 [math]n[/math] まで、 [math]n[/math] 回繰り返す評価方法です。

リーブ・ワン・アウト・クロス・バリデーションは、[math]k[/math]-フォールド・クロス・バリデーションの分割数 [math]k[/math] がデータ数 [math]n[/math] に等しいときと同じで、データが少ないときに用いられます。

リーブ・ワン・アウト・クロス・バリデーションを行うには、sklearn.model_selectionクラスのcross_val_score関数を用いて、cvオプションにsklearn.model_selectionクラスのLeaveOneOut関数を用いて生成したクロス・バリデーション生成器を指定し、結果のスコア配列の平均を求めます。

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
scores = cross_val_score(clf, X, y, cv=loo)
scores.mean()

リーブ・ワン・アウト・クロス・バリデーションを行なったところ、平均正解率は97.3%でした。

↑

グリッド探索による学習パラメーターの最適化 †

今、検討しているのは、決定木の深さは、3がいいのか、4がいいのか、それとも2でもいいのか、評価基準はジニ係数がいいのか、情報量利得がいいのか、ということでした。

sklearn.model_selection.GridSearchCVは、複数の学習パラメーターを組み合わせてクロス・バリデーションを行い、最も良い学習パラメーターを探してくれます。

GridSearchCVには、学習器、学習パラメーターの辞書、[math]k[/math]-フォールド・クロス・バリデーションの分割数 [math]k[/math] を指定します（上と同じようにすれば、リーブ・ワン・アウト・クロス・バリデーションもできます）。

from sklearn.model_selection import GridSearchCV
clf = DecisionTreeClassifier()
params = {'criterion':('gini', 'entropy'), 'max_depth':[1, 2, 3, 4, 5]}
gscv = GridSearchCV(clf, params, cv=5)
gscv.fit(X, y)

fit関数を実行すると、すべての学習パラメーターの組み合わせでクロス・バリデーションを行い、最もスコアが高いパラメーターを best_params_ に、そのときのスコアを best_score_ に格納します。

次のようにして、最も良い学習パラメーターを取り出すことができます。

print('%.3f  %r' % (gscv.best_score_, gscv.best_params_))

すると、次のように出力されます。

0.973  {'criterion': 'gini', 'max_depth': 2}

評価基準はジニ係数、決定木の深さは2が最も良い学習パラメーターであることがわかりました。

しかし、実は、これは結果としては正しいのですが、こう結論付けてしまうのは正しくありません。 すべての学習パラメーターの組み合わせと、そのスコアを出力してみましょう。

X = df_iris_test.values
p = gscv.predict(X)

すると、次のように出力されました。

scores = gscv.cv_results_['mean_test_score']
params = gscv.cv_results_['params']
for score, param in zip(scores, params):
  print('%.3f  %r' % (score, param))

評価基準はジニ係数でも情報量利得でも変わらず、木の深さは1はダメだけど、2から5では変わらないことがわかります。

トップ   新規 一覧 単語検索 最終更新   ヘルプ   最終更新のRSS