バイオ・データ・マイニング/Rでスペクトラル・クラスタリングを使う のバックアップ(No.4)

はじめに †

『Rによるバイオインフォマティクスデータ解析』の7.10節「スペクトラル・クラスタリング」を参考にして，スペクトラル・クラスタリングを行います．

↑

準備 †

Rのインストールについては，次のページを見てください．

[math]k[/math]平均法が苦手なデータとして，二重円のデータを作成します． [math]-4[/math]から[math]4[/math]までの二次元の一様乱数を1,000個生成し，半径[math]3[/math]から[math]4[/math]の範囲にあるデータを[math]c_2[/math]，半径[math]1[/math]から[math]2[/math]の範囲にあるデータを[math]c_1[/math]とします．

x = runif(1000) * 8 - 4
y = runif(1000) * 8 - 4
data = cbind(x, y)
c2 = (x^2 + y^2) < 16 & (x^2 + y^2) > 9
c1 = (x^2 + y^2) <  4 & (x^2 + y^2) > 1
logo = data[(c2 | c1),]
plot(logo)
logo.png

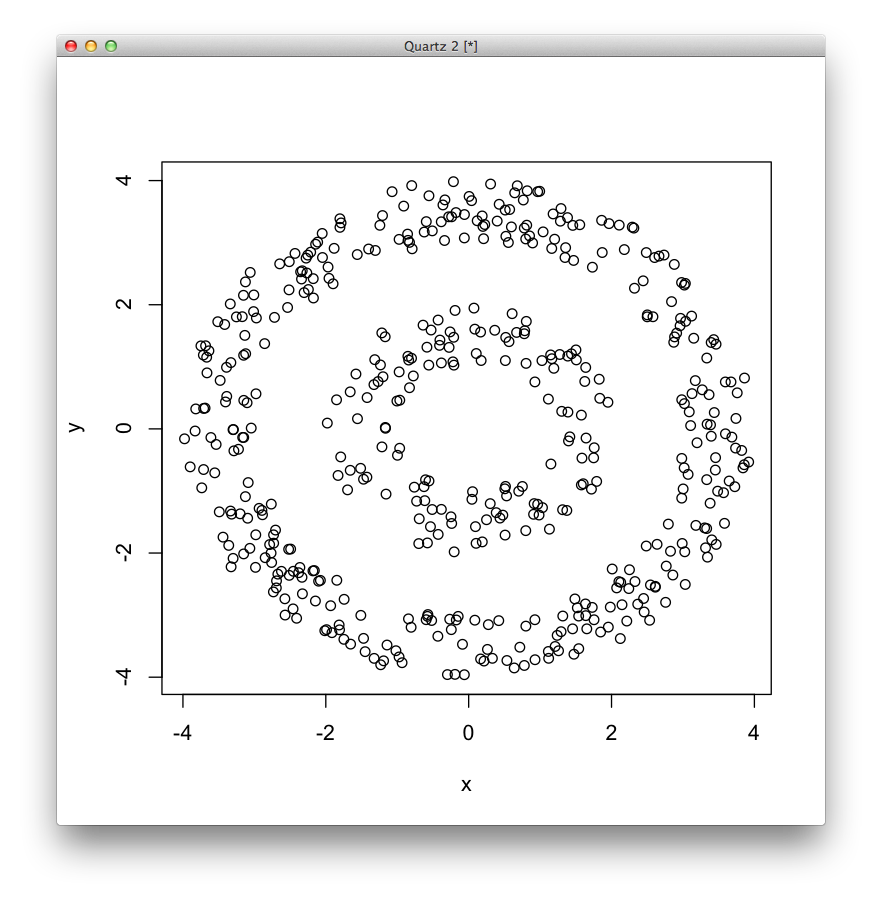
まずは[math]k[/math]平均法を試して見ます．

km = kmeans(logo, 2)
plot(logo, col=km$cluster, pch=km$cluster)
logo_kmeans.png

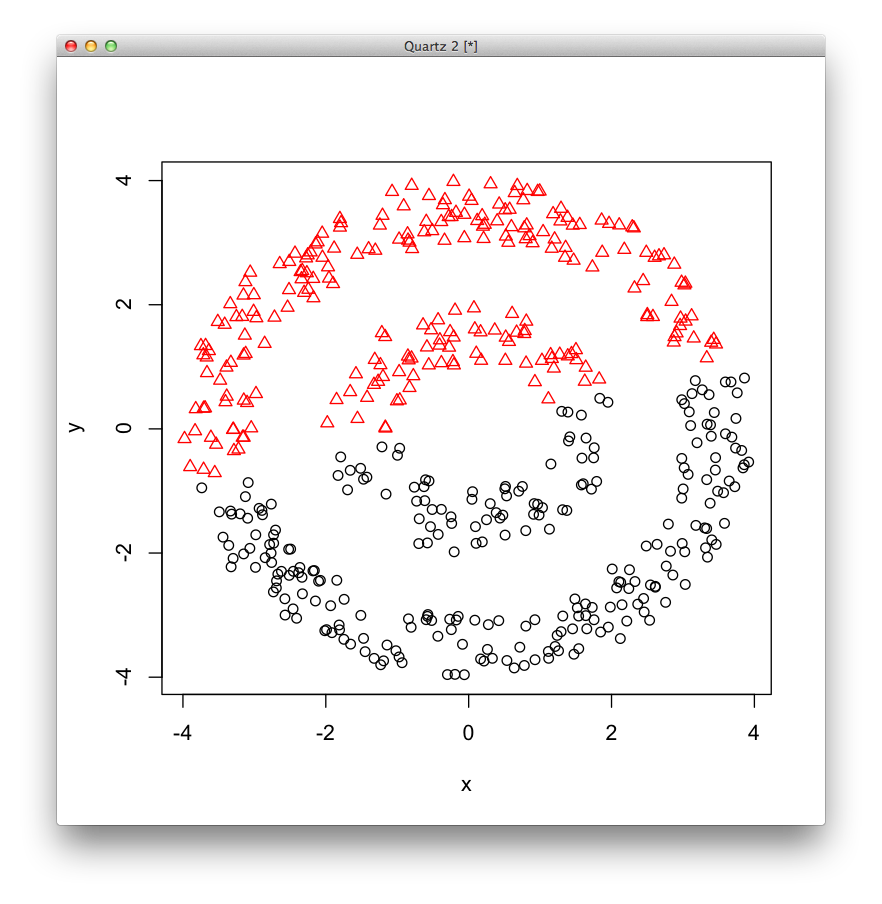
やはり[math]k[/math]平均法ではうまくクラスタリングできません．

スペクトラル・クラスタリングは，kernlabパッケージで提供されています． そこで，kernlabパッケージをインストールします．install.packagesコマンドを実行すると，パッケージをダウンロードするサーバーを聞かれますので，リストからJapanのどれかを選択します．

install.packages("kernlab")
library(kernlab)
↑

スペクトラル・クラスタリング †

スペクトラル・クラスタリングは，距離行列（類似度行列）を次元削減してそこで[math]k[/math]平均法などのクラスタリングを行う手法です．

スペクトラル・クラスタリングを行うには，speccコマンドを用います． speccコマンドには，データとクラスター数を引数として与えます．

sc = specc(logo, center=2)
plot(logo, col=sc, pch=sc)
logo_specc.png

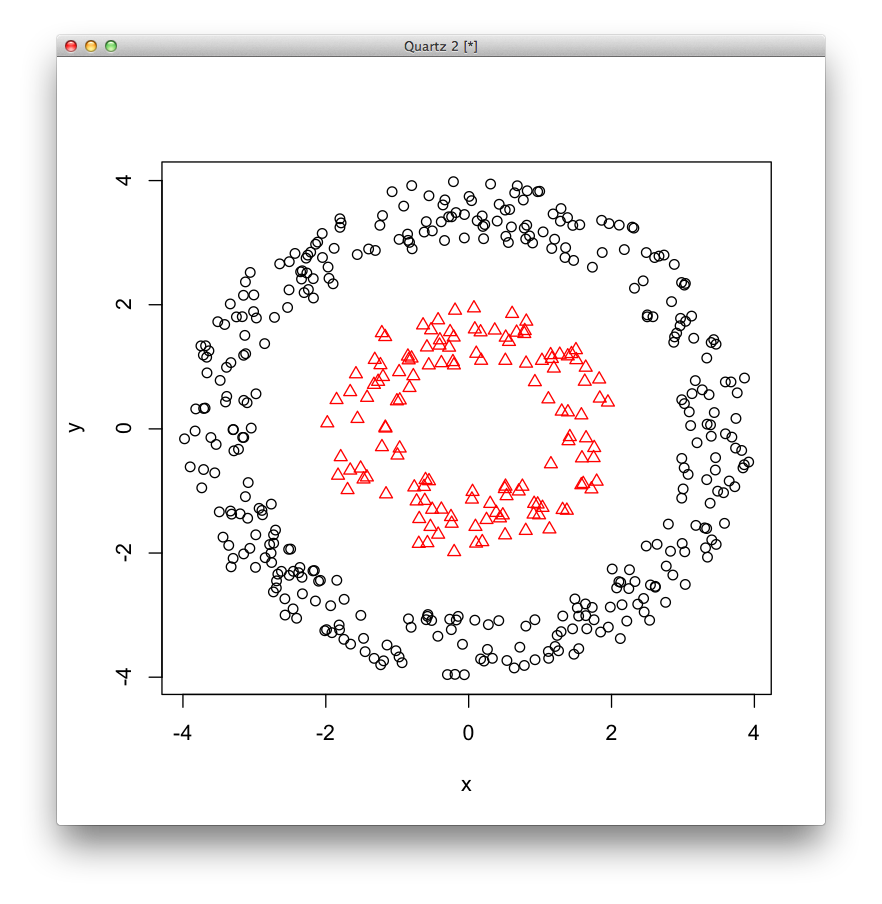
スペクトラル・クラスタリングではきれいにクラスタリングできました．

サンプル・データのspiralsでも試してみます．

data(spirals)
plot(spirals)
spirals.png

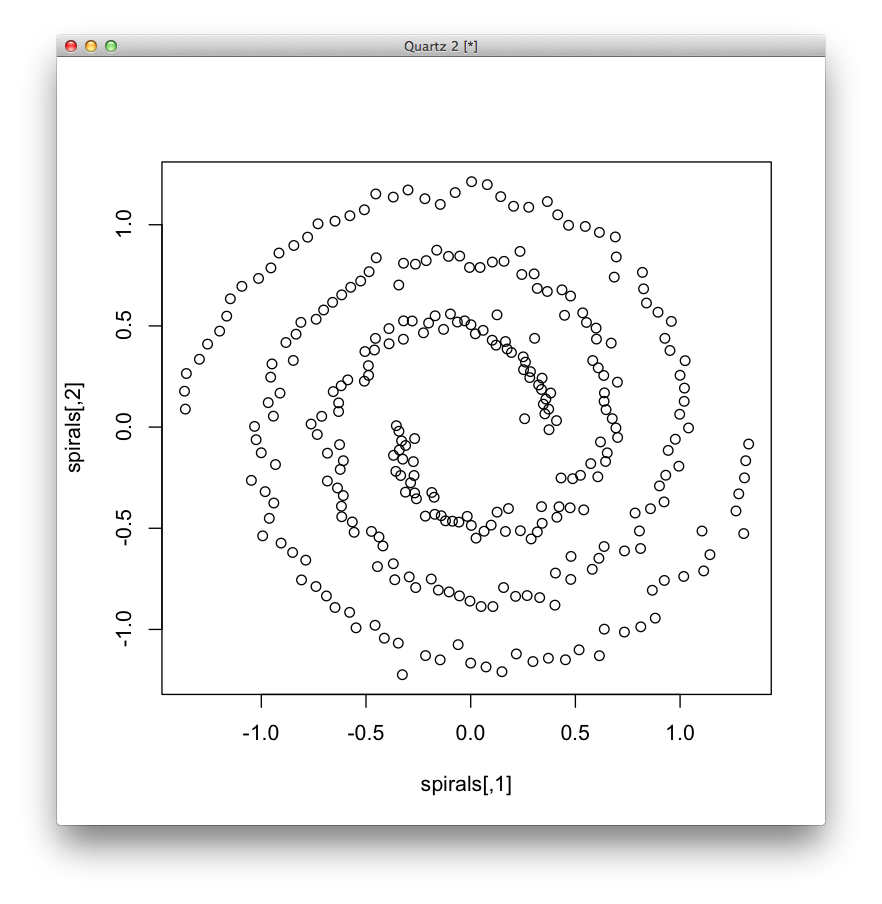
まず，[math]k[/math]平均法を試します．

km = kmeans(spirals, 2)
plot(spirals, col=km$cluster, pch=km$cluster)
spirals_kmeans.png

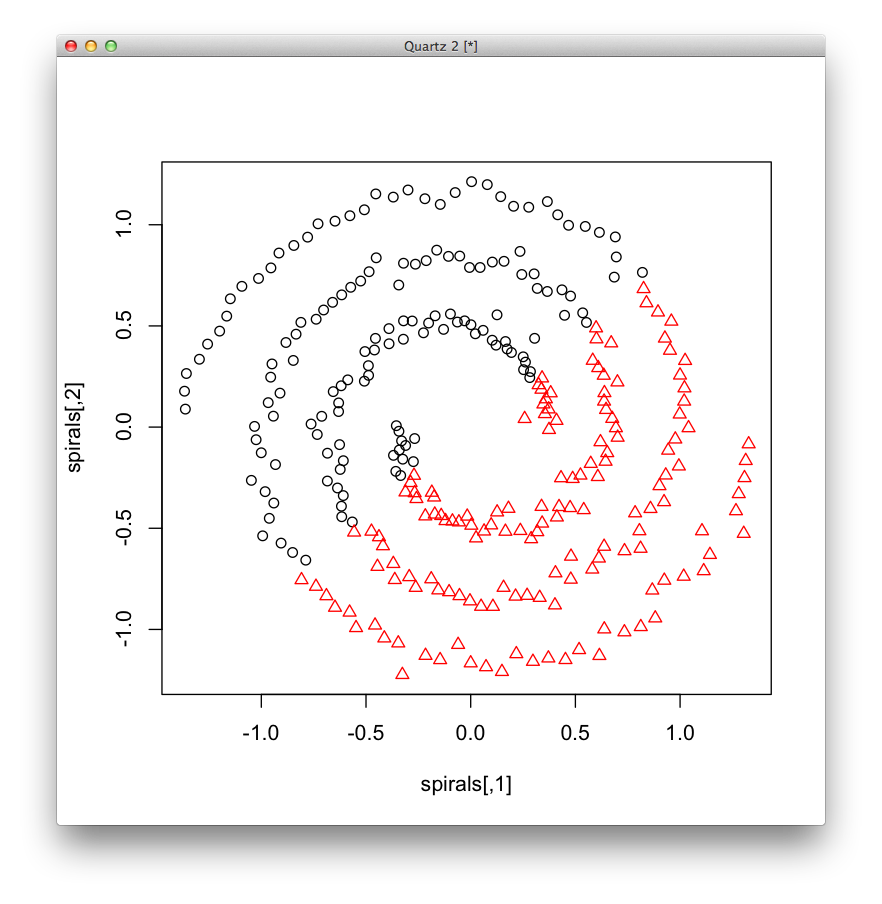
次に，スペクトラル・クラスタリングを用います．

sc = specc(spirals, center=2)
plot(spirals, col=sc, pch=sc)
spirals_specc.png

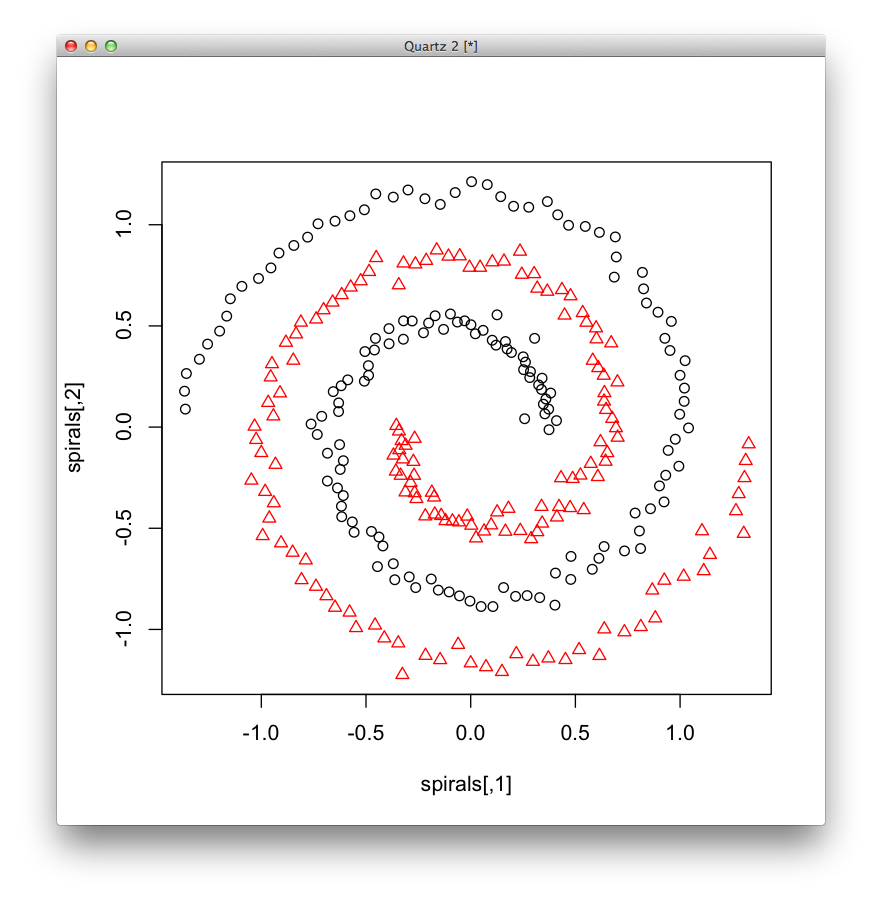
speccは内部でランダムな初期化を行っていますので，[math]k[/math]平均法と同様に，乱数のシードによって結果が変わります． 同じ結果を得るためには，seed.setを用いて乱数のシードを指定してからスペクトラル・クラスタリングを行います．

set.seed(0)
sc = specc(spirals, center=2)
↑

irisデータセット †

irisデータセットでもやってみましょう．

data(iris)

このデータセットは，アヤメの種類（Species）を花びらの長さ（Sepal.Length），幅（Lepal.Width），がくの長さ（Petal.Length），幅（Petal.Width）によって分類する問題です． 長さと幅は連続値，種類はsetosa, versicolor, virginicaのいずれかをとる離散値です．

このデータセットには，setosa, versicolor, virginicaという3種類のアヤメについて，それぞれ50個ずつ，合計150個のデータが含まれています． ランダムに10個のデータを選択して，見てみましょう．

iris[sort(sample(1:150,10)),]

ここでは，Speciesを除いた1列目から4列目だけを取り出して使います．

    Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
4            4.6         3.1          1.5         0.2     setosa
22           5.1         3.7          1.5         0.4     setosa
65           5.6         2.9          3.6         1.3 versicolor
97           5.7         2.9          4.2         1.3 versicolor
100          5.7         2.8          4.1         1.3 versicolor
108          7.3         2.9          6.3         1.8  virginica
116          6.4         3.2          5.3         2.3  virginica
122          5.6         2.8          4.9         2.0  virginica
136          7.7         3.0          6.1         2.3  virginica
146          6.7         3.0          5.2         2.3  virginica

4次元データですが，このうちのSepal.LengthとPetal.Lengthだけを取り出して表示します． データを表示するときの色colと形pchにはirisのSpeciesをas.numeric関数で数値化したものを指定します．

iris.nolabel <- iris[1:4]
iris.png

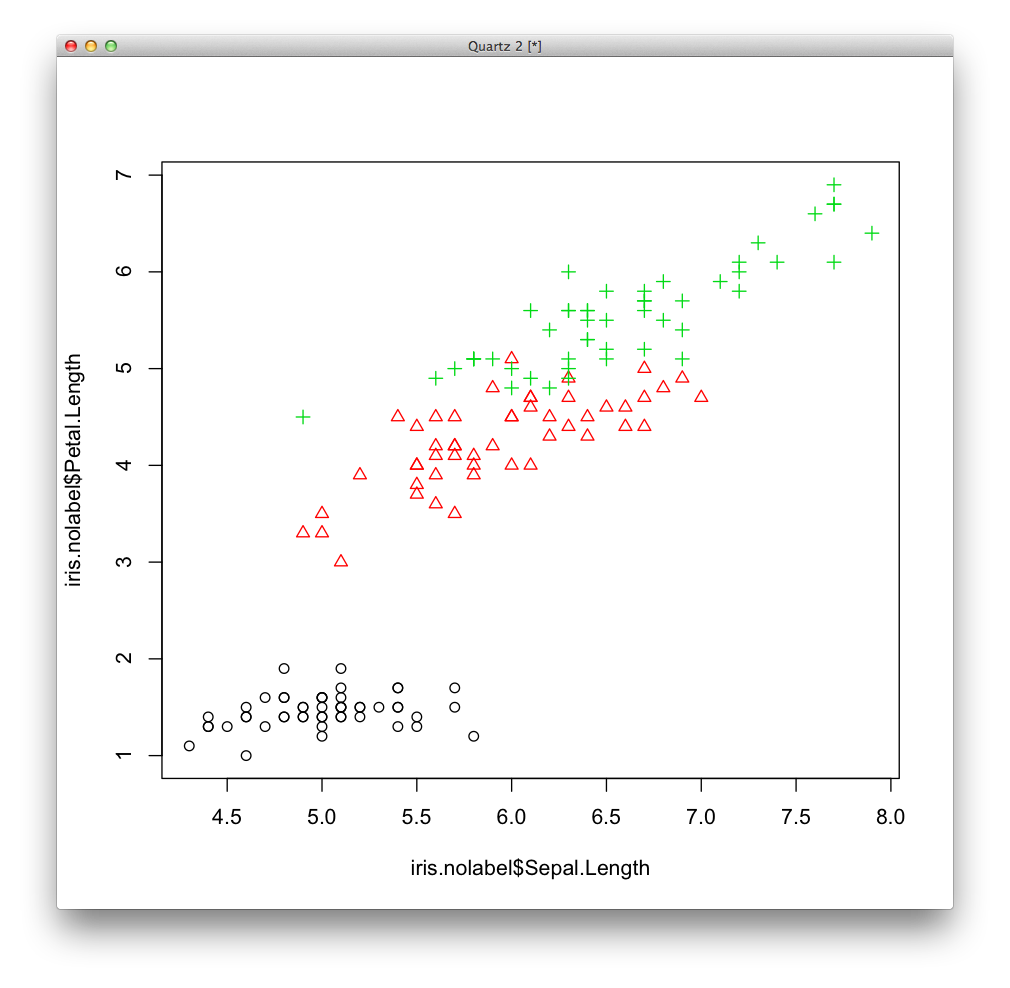
カテゴリーの数は3だとわかっていますので，クラスター数を[math]3[/math]としてスペクトラル・クラスタリングを行います．

plot(iris.nolabel$Sepal.Length, iris.nolabel$Petal.Length,
    col=as.numeric(iris$Species), pch=as.numeric(iris$Species))

今度は色と形をクラスタリングによって得られたクラスター番号によって指定して表示します．

iris.nolabel.specc <- specc(iris.nolabel, center=3)
iris_specc.png

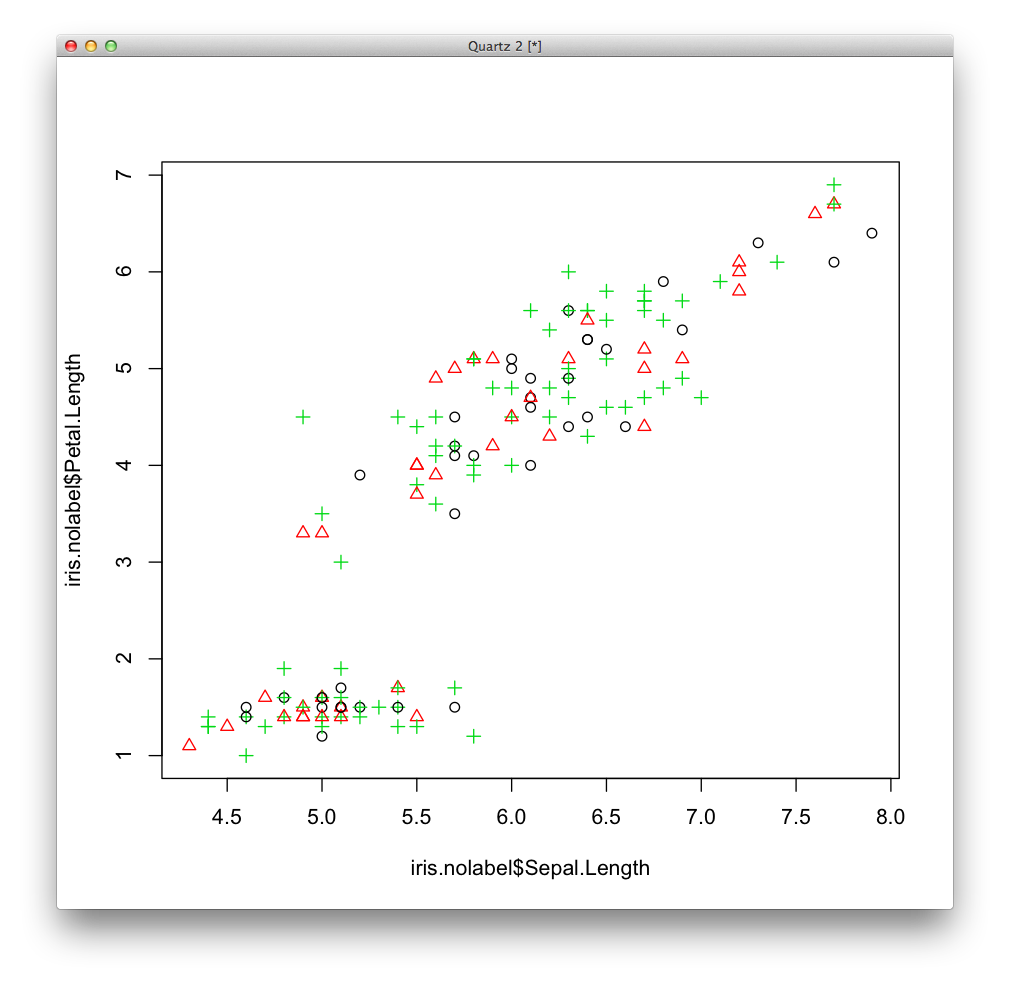
残念ながら，irisデータセットはスペクトラル・クラスタリングではうまくクラスタリングできませんでした．

↑

まとめ †

スペクトラル・クラスタリングは，距離行列（類似度行列）を次元削減してそこで[math]k[/math]平均法などのクラスタリングを行う手法です．

[math]k[/math]平均法が苦手とするようなデータでもうまくいくことがあります．

（内部で行われているクラスタリングが乱数に依存する手法の場合）スペクトラル・クラスタリングの結果は乱数のシードに依存しますので，乱数のシードを変えて実行するとよりよい結果が得られる可能性があります．

↑

参考文献 †

トップ   新規 一覧 単語検索 最終更新   ヘルプ   最終更新のRSS