バイオ・データ・マイニング/Rでk平均法を使う のバックアップ(No.2)

• バックアップ一覧
• 差分 を表示
• 現在との差分 を表示
• ソース を表示
• バイオ・データ・マイニング/Rでk平均法を使う へ行く。
  • 1 (2011-12-12 (月) 18:11:12)
  • 2 (2011-12-12 (月) 19:48:18)
  • 3 (2012-11-27 (火) 14:09:50)
  • 4 (2012-11-28 (水) 09:33:47)
  • 5 (2013-12-20 (金) 12:27:21)
  • 6 (2013-12-23 (月) 09:56:39)
  • 7 (2018-10-25 (木) 10:26:53)

---

この記事はまだ書きかけです．

はじめに †

『Rによるバイオインフォマティクスデータ解析』の7.9.1節「k-menas」を参考にして，k平均法を行います．

準備 †

Rのインストールについては，次のページを見てください．

• MacでRを使う
• WindowsでRを使う

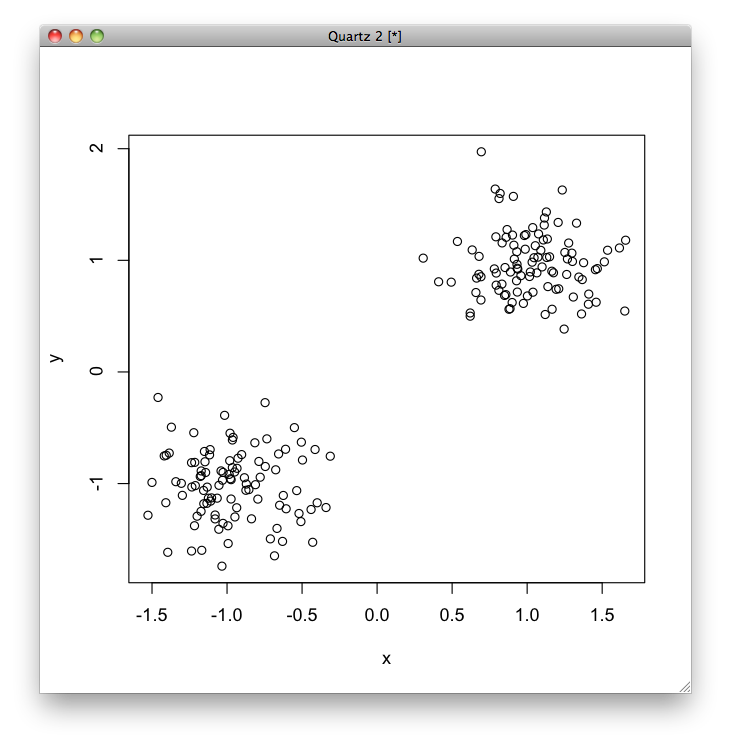
まず，(1, 1) を中心として，x座標とy座標をそれぞれ分散0.3として正規分布で100個の点を生成し，これをc1とします． 次に，(-1 -1) を中心として，同じように分散0.3の正規分布で100個の点を生成し，これをc2とします． c1とc2をまとめて，dataとし，これをプロットします．

set.seed(123)
x1 = rnorm(100, mean=1, sd=0.3)
y1 = rnorm(100, mean=1, sd=0.3)
c1 <- cbind(x1, y1)
x2 = rnorm(100, mean=-1, sd=0.3)
y2 = rnorm(100, mean=-1, sd=0.3)
c2 <- cbind(x2, y2)
data1 <- rbind(c1, c2)
colnames(data1) <- c("x", "y")
plot(data1)

クラスタリング †

クラスタリングは，分類対象のデータ集合をいくつかのグループに分割するものです． 分割された部分データ集合をクラスターといいます．

クラスタリングの手法には，主に階層的アプローチと分割最適化アプローチがあります． ここでは，後者の分割最適化アプローチの一つであるk平均法を行います．

k平均法 †

k平均法（k-means）は，データの集合を k 個のクラスターに分割します． クラスター数 k を最初に決めておかなければなりません．

k平均法は，次の手順で行います．

1. 各データ \bf{x}_1, \dots, \bf{x}_n に対して，ランダムにクラスター c_1, \dots, c_k を割り当てる．
2. クラスター c_1, \dots, c_k ごとに，クラスター c_i に割り当てられたデータの平均を求め，それを c_i の中心とする．
3. 各データ \bf{x}_1, \dots, \bf{x}_n に対して，データ \bf{x}_i と各クラスター c_1, \dots, c_k の中心との距離を求め，\bf{x}_i を最も中心が近いクラスターに割り当て直す．
4. 全てのデータについてクラスターの割り当てが変更されなかったら終了する．そうでない場合は，ステップ2へ戻る．

Rでk平均法を用いるには，kmeans関数を用います． kmeans関数の引数には，分割するデータとクラスター数 k を与えます．

data1.kmeans <- kmeans(data1, 2)

作成されたオブジェクトのcluster変数には割り当てられたクラスター番号が，center変数には各クラスターの中心座標が格納されます．

data1.kmeans$cluster

結果をプロットすると次のようになります．

  [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [26] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [51] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [76] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[101] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[126] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[151] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[176] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

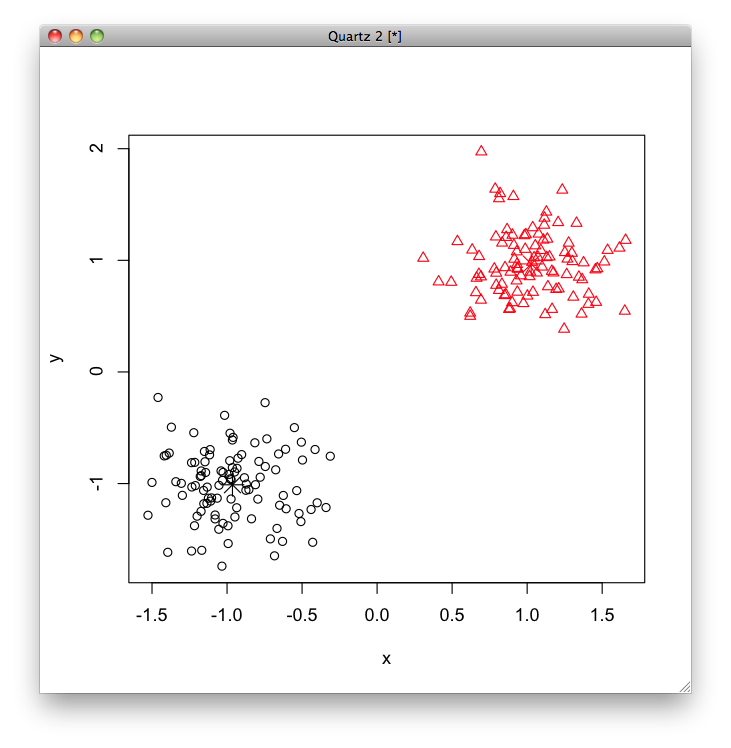
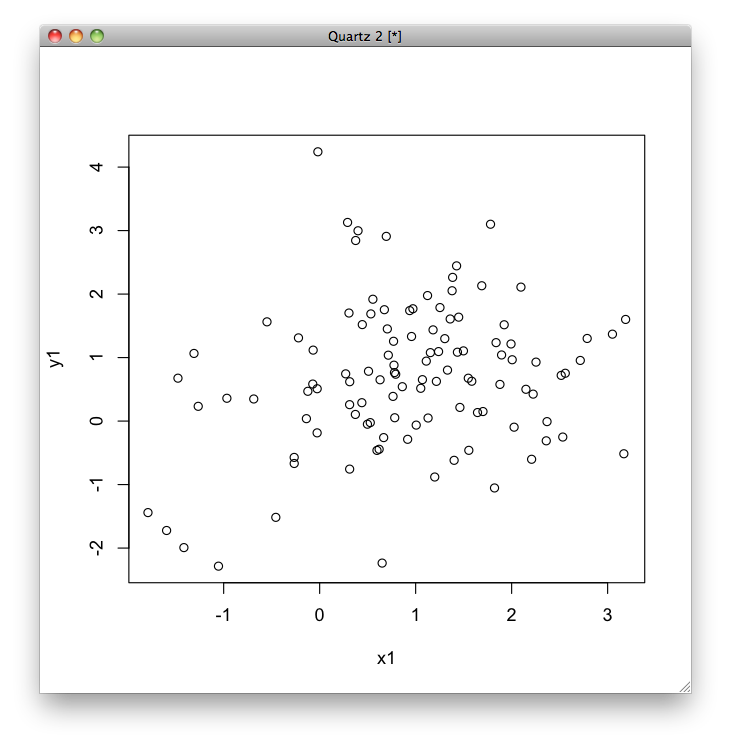
今度は，もう少し分散を大きくし，かつ，データの個数を同じにしないでやってみます．

data1.kmeans$center

           x         y
1 -0.9638605 -1.010867
2  1.0271218  0.967736

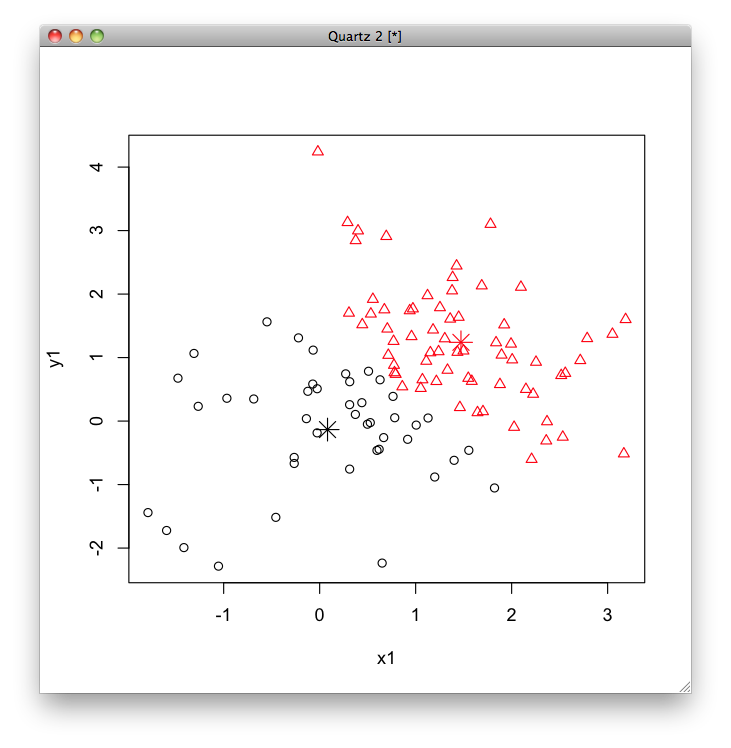
すると，データを生成するときに使用した中心 (1, 1), (-1, -1) よりもずれてしまいました． こういうデータは苦手です．

まとめ †

この記事はまだ書きかけです．

参考文献 †

• クラスタリングとは（クラスター分析とは） - 神嶌敏弘さん