- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rで回帰分析する へ行く。
- 1 (2011-11-07 (月) 13:30:05)
- 2 (2011-11-07 (月) 16:06:30)
- 3 (2011-11-07 (月) 19:24:10)
- 4 (2011-11-08 (火) 02:31:29)
- 5 (2011-11-08 (火) 10:08:16)
- 6 (2011-11-08 (火) 16:54:20)
- 7 (2011-11-08 (火) 19:54:10)
- 8 (2011-11-10 (木) 15:58:47)
- 9 (2011-11-11 (金) 12:46:43)
- 10 (2011-11-12 (土) 17:00:14)
- 11 (2011-11-15 (火) 08:05:02)
- 12 (2013-11-19 (火) 15:52:23)
- 13 (2013-12-05 (木) 13:03:50)
- 14 (2013-12-05 (木) 13:03:50)
- 15 (2013-12-05 (木) 13:03:50)
- 16 (2016-12-15 (木) 08:40:12)
- 17 (2017-12-14 (木) 20:11:02)
- 18 (2017-12-15 (金) 12:11:37)
- 19 (2017-12-15 (金) 12:11:37)
- 20 (2020-01-07 (火) 19:29:34)
- 21 (2020-01-15 (水) 16:27:42)
- 22 (2020-12-23 (水) 13:27:04)
はじめに †
『Rによるバイオインフォマティクスデータ解析』の7.17節LASSOを参考にして,回帰分析をします.
LASSO回帰の前に,線形回帰をやります. また,Ridge回帰もやります.
準備 †
まずは,標準で使用できるirisデータを使います.
data(iris)
このデータは,ユリの種類(Species)を花びらの長さ(Sepal.Length),幅(Lepal.Width),がくの長さ(Petal.Length),幅(Petal.Width)によって分類する問題です. 長さと幅は連続値,種類はsetosa, versicolor, virginicaのいずれかをとる離散値です.
150個のデータが含まれています. 最初の10個を表示すると,次のようになります.
iris[sort(sample(1:150,10)),]
ランダムにサンプリングした10個を表示すると,このようになります.
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
線形回帰(単回帰) †
まず,説明変数が1つの線形回帰(単回帰)を行います.
ここでは,がくの長さ(Petal.Length)を被説明変数(目的変数)として,花びらの長さ(Sepal.Length)を説明変数としてモデルを学習します.
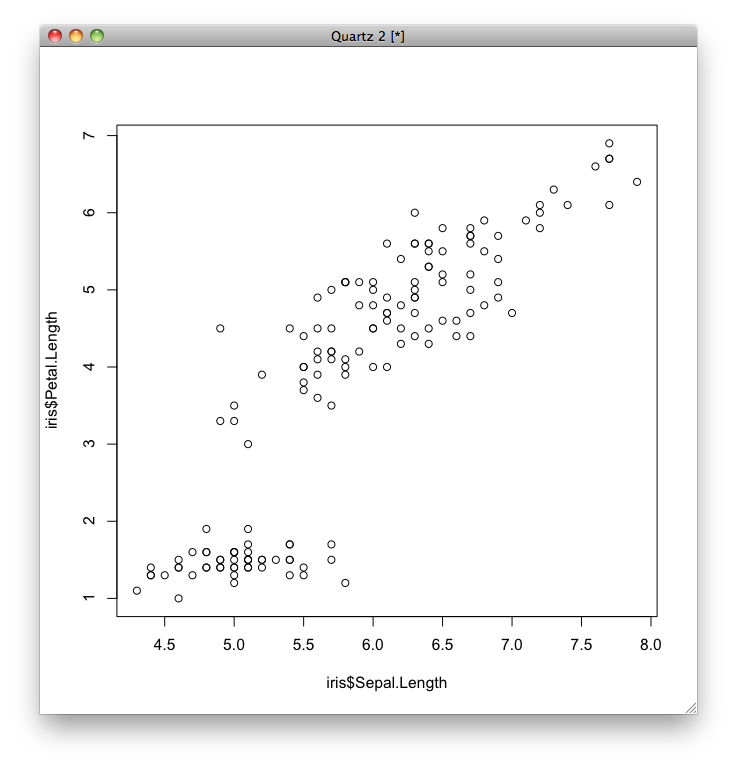
この関係をプロットすると次のようになります.
plot(iris$Sepal.Length, iris$Petal.Length)
Rでは,モデルの式を,記号~を使って「目的変数 ~ 説明変数」というように表します. したがって,目的変数をがくの長さ(iris$Petal.Length),説明変数を花びらの長さ(iris#Sepal.Length)とするとき,モデルの式は「iris$Petal.Length ~ iris$Sepal.Length」となります.
線形回帰は,標準で用意されているlm関数で行います.
y <- iris$Petal.Length x <- iris$Sepal.Length
学習された結果を表示してみると,次のようになります.
model <- lm(y~x)
Coefficientsは係数を表し,Interceptは定数項([mathy[/math]切片)の値を表します. つまり,花びらの長さを[math]x[/math],がくの長さを[math]y[/math]とすると,学習された式は[math]y = 1.858433 x - 7.101443[/math]です.
学習された線形回帰モデルを図示します.
model
すると,次のようなグラフがプロットされます.
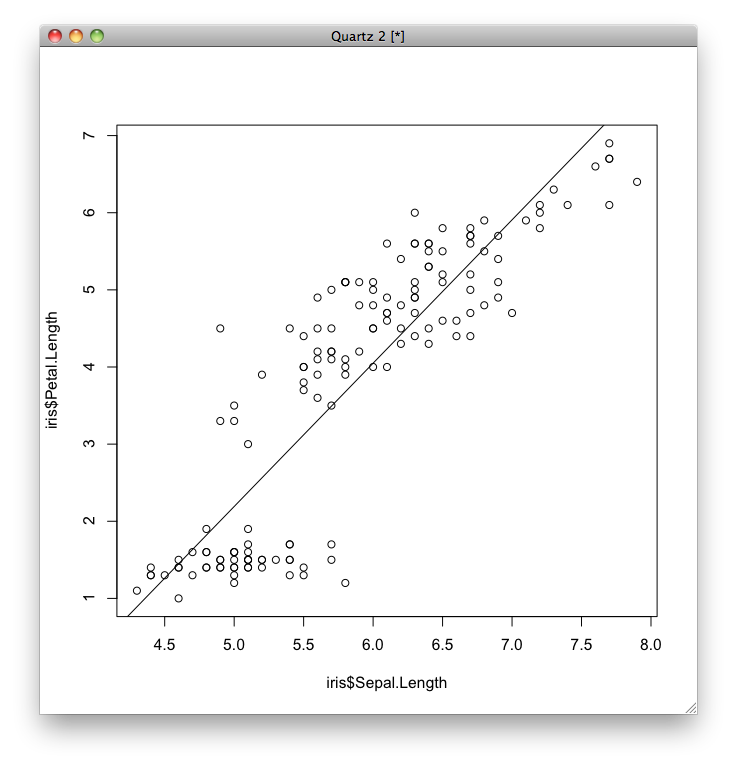
単回帰だとモデルが視覚化しやすいです.
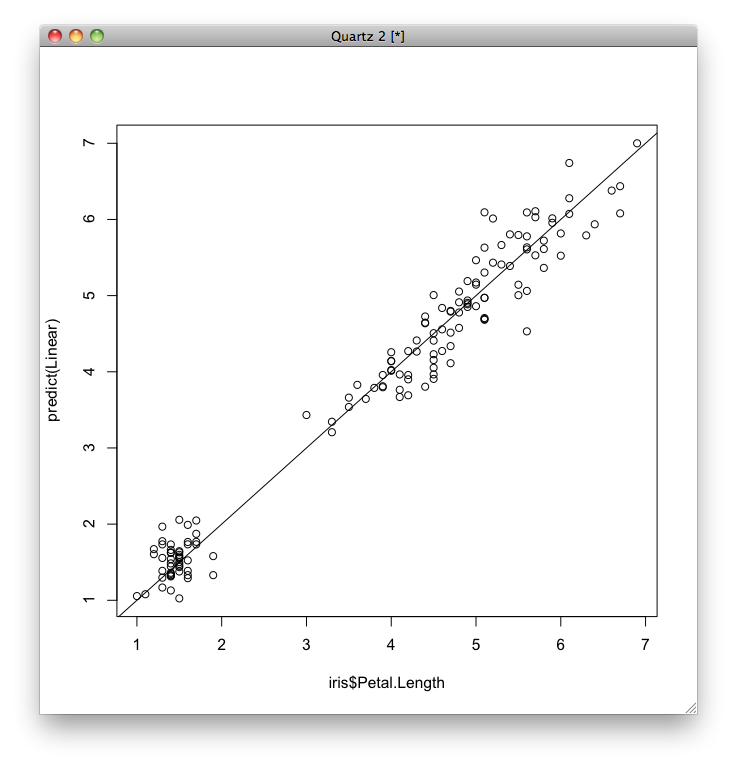
次に,予測誤差を視覚化するため,それぞれのデータについて,横軸に実際のがくの長さ(iris$Petal.Length),縦軸にその予測値をとってグラフを表示します. 予測値はpredict関数で求めることができます.
> model Call: lm(formula = y ~ x) Coefficients: (Intercept) x -7.101 1.858
線形回帰(重回帰) †
説明変数が複数ある回帰を重回帰といいます.
ここでは,がくの長さ(iris$Petal.Length)を目的変数,花びらの長さ(iris$Sepal.Length),幅(iris$Sepal.Width),がくの幅(iris$Petal.Width)を説明変数として重回帰を行います.
説明変数が複数あるときは,モデルを表すときにそれぞれの変数を記号+で連結して表します. ここでは,「iris$Petal.Length ~ iris$Sepal.Length+iris$Sepal.Width+iris$Petal.Width」となります.
単回帰と同じように,lm関数を用いて線形回帰を行います.
plot(x, y) abline(model)
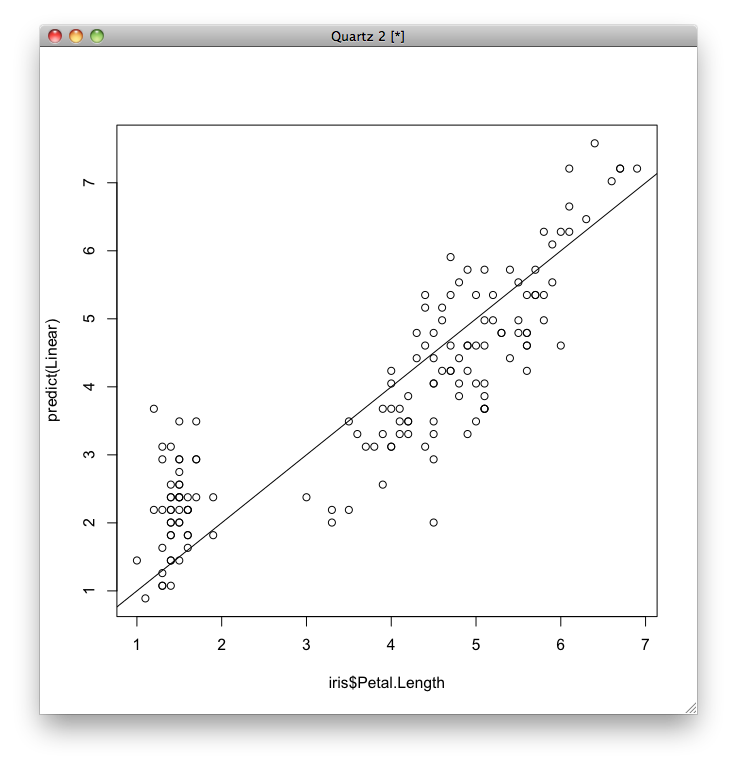
重回帰分析の場合はモデルが視覚化しにくいので,予測誤差だけ視覚化します.
plot(iris$Petal.Length, predict())
abline(a=0,b=1)
単回帰の場合よりも誤差が小さくなっていることがわかります.
LASSO回帰 †
LASSO回帰はglmnetパッケージに含まれています. glmnetパッケージは そこで,glmnetパッケージをインストールして,使用します.
summary(model)
私の環境ではこのような警告が出ますが,これは「utilsパッケージのhead関数とtail関数をgolmnetパッケージのhead関数とtail関数で置き換えましたよ」という意味なので,気にしなくていいです.
LASSO回帰は,glmnetパッケージのglmnet関数を用いて行います. 引数には,説明変数行列,目的変数,そしてオプションを与えます.
> summary(model) Call: lm(formula = y ~ x) Residuals: Min 1Q Median 3Q Max -2.47747 -0.59072 -0.00668 0.60484 2.49512 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -7.10144 0.50666 -14.02 <2e-16 *** x 1.85843 0.08586 21.65 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.8678 on 148 degrees of freedom Multiple R-squared: 0.76, Adjusted R-squared: 0.7583 F-statistic: 468.6 on 1 and 148 DF, p-value: < 2.2e-16
ここで,
この記事はまだ書きかけです.
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)