- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rで階層クラスタリングを使う へ行く。
- 1 (2011-12-01 (木) 13:52:31)
- 2 (2011-12-01 (木) 16:42:56)
- 3 (2011-12-01 (木) 17:04:04)
- 4 (2011-12-02 (金) 16:08:04)
- 5 (2011-12-02 (金) 19:08:30)
- 6 (2012-11-28 (水) 13:53:13)
- 7 (2012-11-29 (木) 09:29:41)
- 8 (2013-12-13 (金) 07:48:50)
- 9 (2013-12-13 (金) 07:48:50)
- 10 (2015-01-09 (金) 11:02:03)
- 11 (2015-12-02 (水) 15:37:17)
- 12 (2016-11-30 (水) 14:41:58)
- 13 (2018-10-25 (木) 16:32:15)
- 14 (2018-10-25 (木) 17:34:00)
- 15 (2020-12-09 (水) 15:03:19)
はじめに †
『Rによるバイオインフォマティクスデータ解析』の7.8節「階層クラスタリング」を参考にして、階層クラスタリングを行います。
準備 †
Rのインストールについては、次のページを見てください。
ここでは、標準で使用できるirisデータセットを使います。
data(iris)
このデータセットは、アヤメの種類(Species)をがく片の長さ(Sepal.Length)、幅(Sepal.Width)、花びらの長さ(Petal.Length)、幅(Petal.Width)によって分類する問題です。 長さと幅は連続値、種類はsetosa, versicolor, virginicaのいずれかをとる離散値です。
このデータセットには、setosa, versicolor, virginicaという3種類のアヤメについて、それぞれ50個ずつ、合計150個のデータが含まれています。 ランダムに10個のデータを選択して、見てみましょう。
iris[sort(sample(1:150,10)),]
クラスタリング †
クラスタリングは、分類対象のデータ集合をいくつかのグループに分割するものです。 分割された部分データ集合をクラスターといいます。
クラスタリングの手法には、主に階層的アプローチと分割最適化アプローチがあります。 ここでは、前者の階層的アプローチを行います。
階層クラスタリング †
階層クラスタリングには、トップ・ダウンに階層化する分岐型とボトム・アップに階層化する凝集型があります。 ここでは、後者の凝集型をやります。
凝集型階層クラスタリングでは、まず、1つのデータだけを含むクラスターをデータと同じ数だけ作ります。 それから、最も近い(似ている)クラスター同士を結合してより大きい新しいクラスターを作ります。 これを全てのクラスターが一つに結合されるまで繰り返します。
Rで階層クラスタリングを用いるには、hclust関数を用います。 hclust関数の引数には距離行列を与えます。 距離行列は、dist関数で求めることができます。
そこで、まず、irisデータのSepal.Length, Sepal.Width, Petal.Length, Petal.Widthの値から、距離行列を計算します。
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
この距離行列を用いて、階層クラスタリングを行います。
d <- dist(iris[,1:4])
結果をplot関数を用いてプロットするとデンドログラムと呼ばれる図が描かれます。
model <- hclust(d)
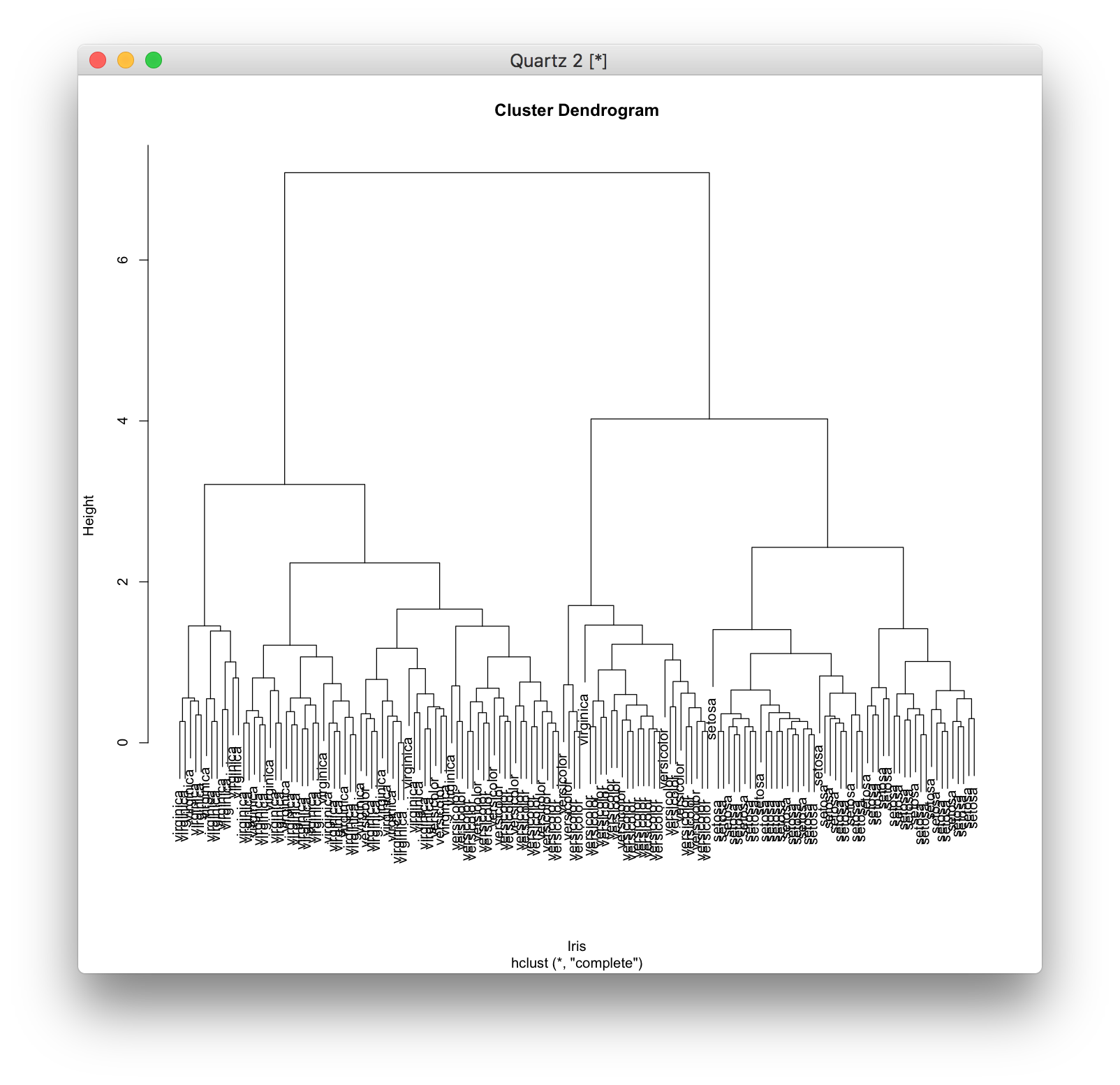
デンドログラムを見ると、どのクラスターが結合したのかがわかります。
距離 †
上でも説明したように、凝集型階層クラスタリングでは最も近い(似ている)クラスター同士をくっつけますが、近いか遠いかを決めるのに、距離尺度が必要になります。
一般的な距離尺度としては、ユークリッド距離が用いられています。 \[ d({\bf x}_1, {\bf x}_2) = \sqrt{ \sum_{i=1}^p \left( x_{2,i} - x_{1,i} \right)^2 } \]
距離行列を求めるときにmethodオプションを指定しなければ、ユークリッド距離の距離行列になります。
plot(model, labels=iris[,5], xlab="Iris")
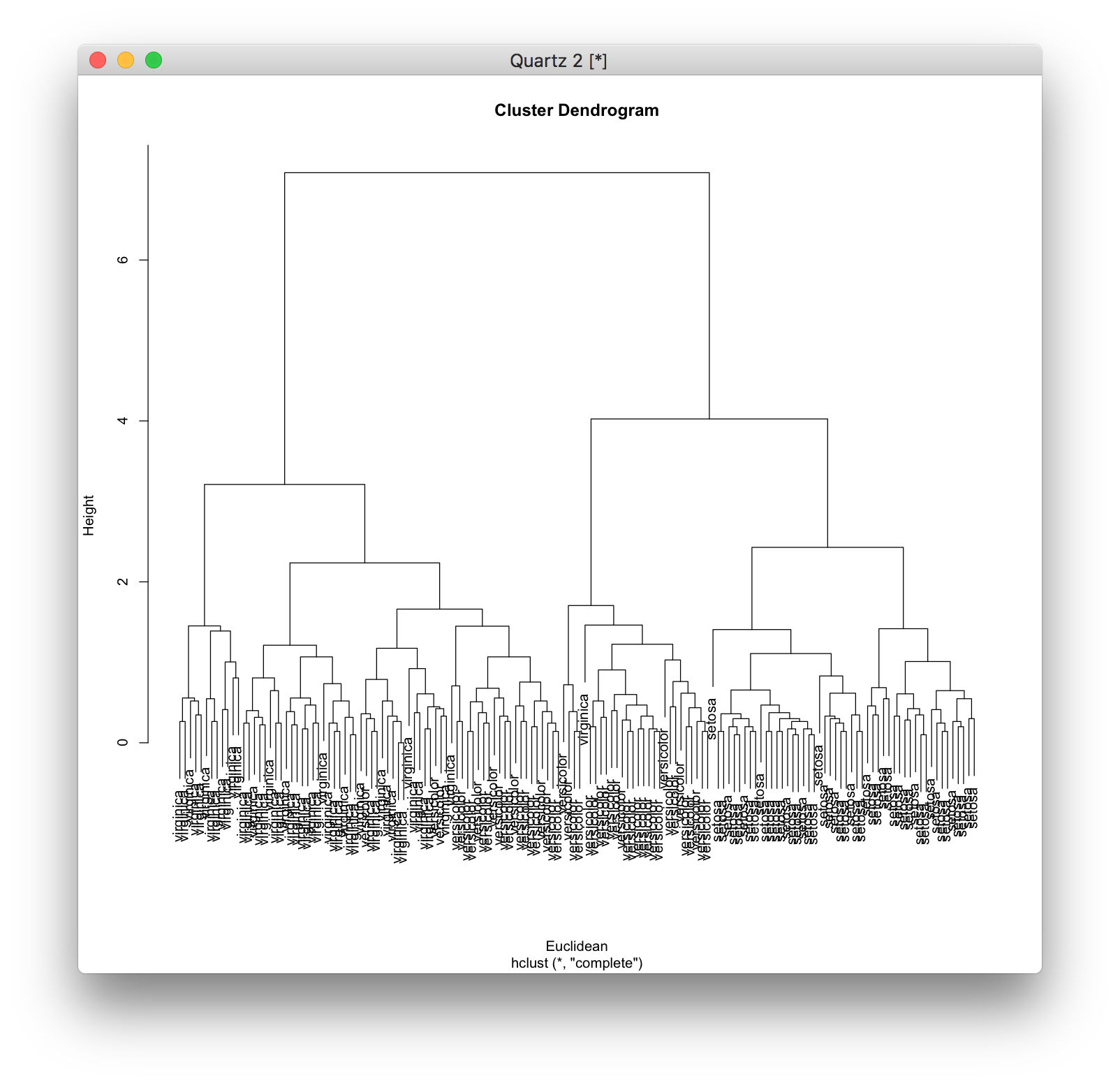
ユークリッド距離の他に、マンハッタン距離(マンハッタンでのタクシーを利用するときのように、一つの軸と並行に移動することしかできないときの移動距離) \[ d({\bf x}_1, {\bf x}_2) =\sum_{i=1}^p \left| x_{2,i} - x_{1,i} \right| \] を使うこともできます。 マンハッタン距離を使うには、dist関数にオプションmethod="manhattan"を指定します。
d <- dist(iris[,1:4]) model <- hclust(d) plot(model, labels=iris[,5], xlab="Euclidean")
この他にも、いくつもの距離尺度が提案されています。 類似度と距離尺度に付いてはこちらにたくさんまとめられています。
- 類似度と距離 - CatTail Wiki*
結合方式 †
ユークリッド距離もマンハッタン距離も二つのデータ同士の間の距離を表していますが、どのクラスターとどのクラスターが最も近い(似ている)のかを直接的には表していません。
求めた距離に基づいて、どのクラスターとどのクラスターを結合するのかを決めなくてはなりません。 これが結合方式です。
上の二つの例でも用いられた標準の方式は完全連結法 (complete linkage method) という方式で、クラスター[math]C_1[/math]に含まれるデータとクラスター[math]C_2[/math]に含まれるデータの間の距離の中で最大のもの(つまり、最も離れているもの)を[math]C_1 C_2[/math]間の距離として、最も近い(似ている)クラスターを結合します。 \[ d(C_1, C_2) = \max_{{\bf x}_1 \in C_1, {\bf x}_2 \in C_2} d({\bf x}_1, {\bf x}_2) \]
単連結法 (single linkage method) では、反対に、クラスター[math]C_1[/math]に含まれるデータとクラスター[math]C_2[/math]に含まれるデータの間の距離の中で最小のもの(つまり、最も近いもの)を[math]C_1 C_2[/math]間の距離として、最も近い(似ている)クラスターを結合します。 \[ d(C_1, C_2) = \min_{{\bf x}_1 \in C_1, {\bf x}_2 \in C_2} d({\bf x}_1, {\bf x}_2) \] 単連結法を用いるには、hclust関数にオプションmethod="single"を指定します。
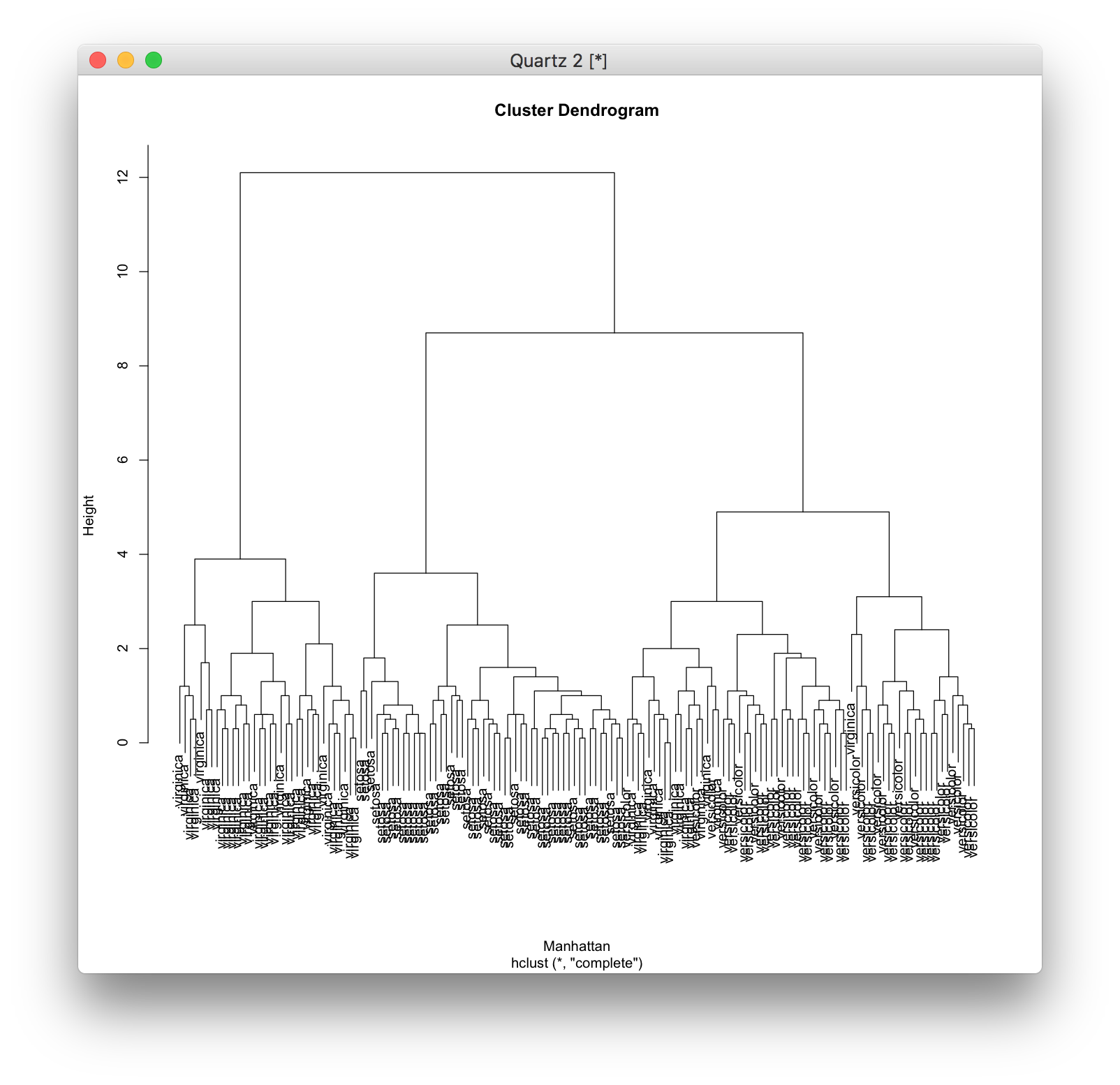
d <- dist(iris[,1:4], method="manhattan") model <- hclust(d) plot(model, labels=iris[,5], xlab="Manhattan")
群平均法 (group average method) では、クラスター[math]C_1[/math]に含まれるデータとクラスター[math]C_2[/math]に含まれるデータの間の距離の平均を[math]C_1 C_2[/math]間の距離として最も近い(似ている)クラスターを結合します。 \[ d(C_1, C_2) = \frac{1}{|C_1||C_2|} \sum_{{\bf x}_1 \in C_1} \sum_{{\bf x_2} \in C_2} d({\bf x}_1 {\bf x}_2) \] hclust関数にオプションmethod="average"と指定すると、群平均法による結合になります。 参考にしている『Rによるバイオインフォマティクスデータ解析』には、クラスターに含まれるデータの平均同士の距離をクラスター同士の距離としているように書かれていますが、この説明は間違っています。
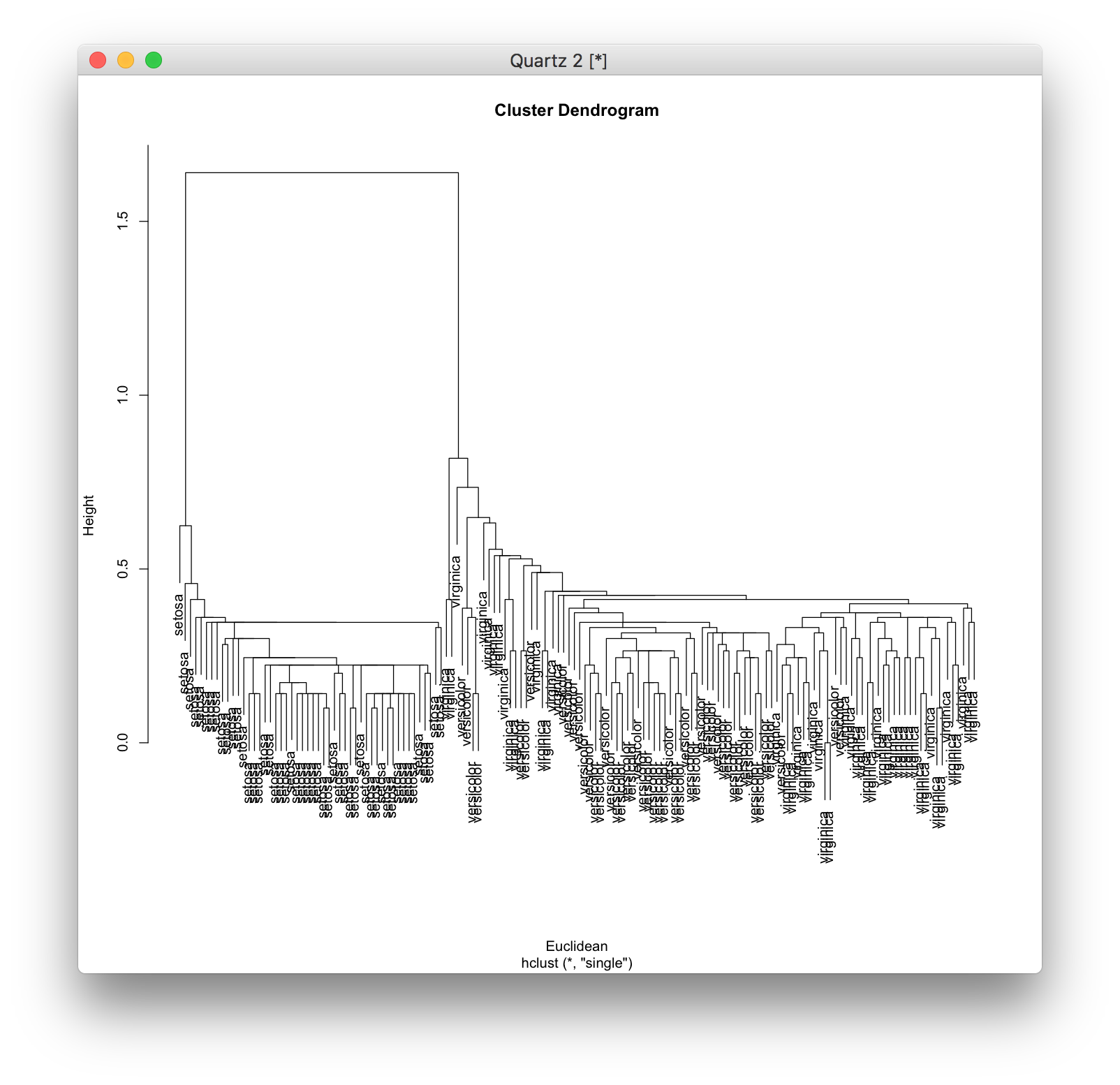
d <- dist(iris[,1:4]) model <- hclust(d, method="single") plot(model, labels=iris[,5], xlab="Euclidean")
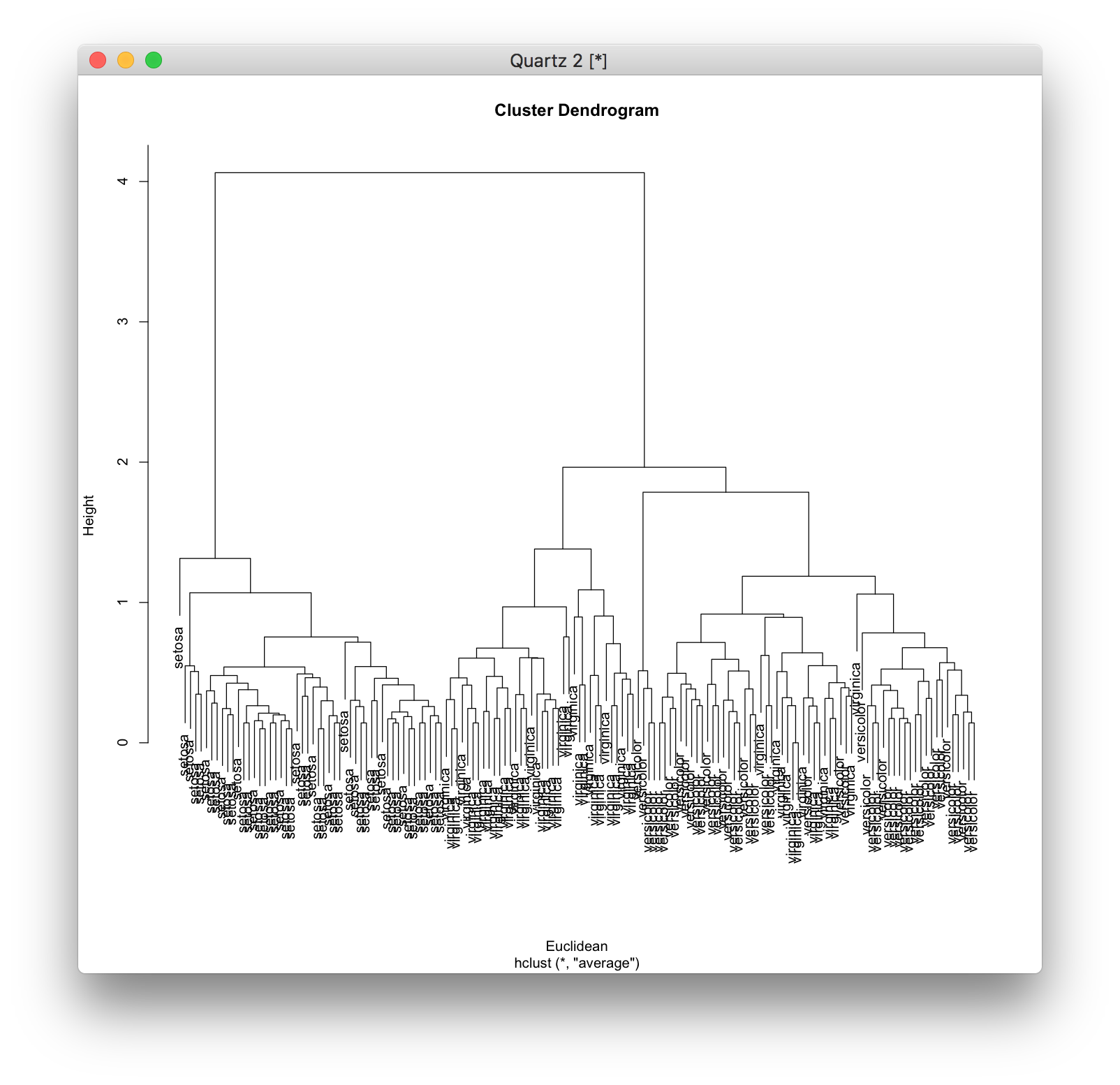
メジアン法 (median linkage method) では、クラスター[math]C_1[/math]に含まれるデータの中央値とクラスター[math]C_2[/math]に含まれるデータの中央値の間の距離を[math]C_1 C_2[/math]間の距離として、最も近い(似ている)クラスターを結合します。 メジアン法を用いるには、hclust関数にオプションmethod="median"を指定します。
d <- dist(iris[,1:4]) model <- hclust(d, method="average") plot(model, labels=iris[,5], xlab="Euclidean")
#ref(): File not found: "usarrests_hclust_median_euclidean.png" at page "バイオ・データ・マイニング/Rで階層クラスタリングを使う"
重心法 (centroid linkage method) では、クラスター[math]C_1[/math]の重心とクラスター[math]C_2[/math]の重心の間の距離を[math]C_1 C_2[/math]間の距離として、最も近い(似ている)クラスターを結合します。 \[ d(C_1, C_2) = d({\bf c}_1, {\bf c}_2) \] \[ {\bf c}_{i} = \frac{ \sum_{x \in C_i} x}{|C_i|} \] 重心法を用いるには、hclust関数にオプションmethod="centroid"を指定します。
d <- dist(iris[,1:4]) model <- hclust(d, method="median") plot(model, labels=iris[,5], xlab="Euclidean")
#ref(): File not found: "usarrests_hclust_centroid_euclidean.png" at page "バイオ・データ・マイニング/Rで階層クラスタリングを使う"
Ward法では、クラスター[math]C_1, C_2[/math]を結合してクラスター[math]C_1 \cup C_2[/math]を作ったときに、各データとそれが含まれるクラスターの重心との距離の分散の増分を[math]C_1 C_2[/math]間の距離として、最も近い(似ている)クラスターを結合します。 \[ d(C_1, C_2) = {\mathrm E}(C_1 \cup C_2) - {\mathrm E}(C_1) - {\mathrm E}(C_2) \] \[ {\mathrm E}(C_i) = \sum_{{\bf x} \in C_i} (d({\bf x}, {\bf c_i}))^2 \] Ward法を用いるには、hclust関数にオプションmethod="ward.D"を指定します(新しい"ward.D2"という方法もあります)。
d <- dist(iris[,1:4]) model <- hclust(d, method="centroid") plot(model, labels=iris[,5], xlab="Euclidean")
#ref(): File not found: "usarrests_hclust_ward_euclidean.png" at page "バイオ・データ・マイニング/Rで階層クラスタリングを使う"
距離行列 †
hclustでは、距離行列を自分で作成して階層クラスタリングを行うことができます。 距離行列は、(対角要素を除いた)下三角行列からas.distを用いて作成します。
ここでは、例として、A, B, C, Dという4つのデータを含む距離行列を作成します。
まず、名前のベクトルを作成します。
d <- dist(iris[,1:4]) model <- hclust(d, method="ward.D") plot(model, labels=iris[,5], xlab="Euclidean")
つぎに、4次の正方行列を作成します。
names = c("A", "B", "C", "D")
対角要素以外の下三角行列の要素に、各データ間の距離を代入します。
d = matrix(, 4, 4, dimnames=list(names, names))
このデータは、一直線上に並べることができ、Aを0とすると、Bが1、Cが5、Dが6の位置にあります。
as.distを用いてこの正方行列を距離行列に変換できることを確認します。
> d A B C D A NA NA NA NA B NA NA NA NA C NA NA NA NA D NA NA NA NA
この距離行列をhclustに引数として与えることで、階層クラスタリングができます。
d[2,1] = 1 d[3,1] = 5 d[4,1] = 6 d[3,2] = 4 d[4,2] = 5 d[4,3] = 3
#ref(): File not found: "dist_hclust.png" at page "バイオ・データ・マイニング/Rで階層クラスタリングを使う"
クラスター番号 †
階層クラスタリングによってつけられたクラスター番号を調べるには、cutree関数を使います。 cutree関数には、hclust関数によって出力された結果とクラスター数を与えます。
> d A B C D A NA NA NA NA B 1 NA NA NA C 5 4 NA NA D 6 5 3 NA
これはWard法による階層クラスタリングの結果をクラスター数を3として分けたときのそれぞれの州が属するクラスター番号です。
まとめ †
凝集型階層クラスタリングでは、最も近いクラスターを結合して新しいクラスターを作成することを繰り返すことによってクラスタリングを行います。
このとき、最も近い2つのクラスターを選び出すために、クラスター間の距離を測る必要があります。 クラスター間の距離尺度の違いにより、完全結合法、単結合法、群平均法、メジアン法、重心法、Ward法という方法に分かれます。
また、クラスター間の距離尺度はデータ間の距離尺度に基づいているため、データ間の距離も測る必要があります。 データ間の距離尺度には、ユークリッド距離、マンハッタン距離、マハラノビス距離、コサイン係数などがあります。
したがって、凝集型階層型クラスタリングでは、データ間の距離尺度とクラスター間の距離尺度の二つを選択することになります。
演習 †
irisデータに対して、Speciesの列を取り除き、1列目から4列目だけを取り出して階層クラスタリングをやってみよう。
irisデータから1列目から4列目だけを取り出すには、次のようにします。
as.dist(d)
参考文献 †
- クラスタリングとは(クラスター分析とは) - 神嶌敏弘さん
- 類似度と距離 - CatTail Wiki*
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)