- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rでk平均法を使う へ行く。
はじめに †
『Rによるバイオインフォマティクスデータ解析』の7.9.1節「[math]k[/math]-menas」を参考にして,[math]k[/math]平均法を行います.
準備 †
Rのインストールについては,次のページを見てください.
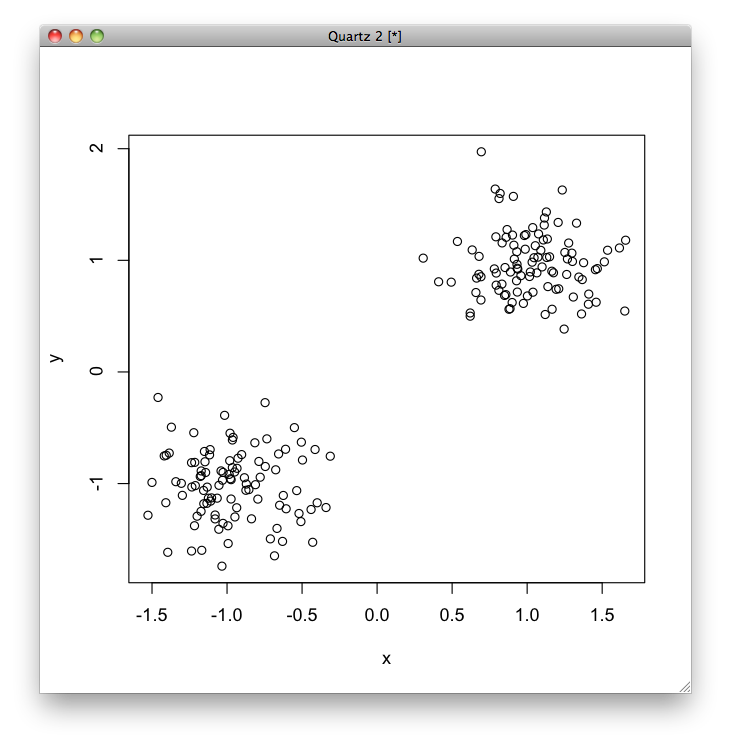
まず,[math](1, 1)[/math] を中心として,[math]x[/math]座標と[math]y[/math]座標をそれぞれ分散0.3として正規分布で100個の点を生成し,これをc1とします. 次に,[math](-1 -1)[/math] を中心として,同じように分散0.3の正規分布で100個の点を生成し,これをc2とします. c1とc2をまとめて,dataとし,これをプロットします.
set.seed(123) x1 = rnorm(100, mean=1, sd=0.3) y1 = rnorm(100, mean=1, sd=0.3) c1 <- cbind(x1, y1) x2 = rnorm(100, mean=-1, sd=0.3) y2 = rnorm(100, mean=-1, sd=0.3) c2 <- cbind(x2, y2) data1 <- rbind(c1, c2) colnames(data1) <- c("x", "y") plot(data1)
クラスタリング †
クラスタリングは,分類対象のデータ集合をいくつかのグループに分割するものです. 分割された部分データ集合をクラスターといいます.
クラスタリングの手法には,主に階層的アプローチと分割最適化アプローチがあります. ここでは,後者の分割最適化アプローチの一つである[math]k[/math]平均法を行います.
k平均法 †
[math]k[/math]平均法([math]k[/math]-means)は,データの集合を [math]k[/math] 個のクラスターに分割します. クラスター数 [math]k[/math] を最初に決めておかなければなりません.
[math]k[/math]平均法は,次の手順で行います.
- 各データ [math]\bf{x}_1, \dots, \bf{x}_n[/math] に対して,ランダムにクラスター [math]c_1, \dots, c_k[/math] を割り当てる.
- クラスター [math]c_1, \dots, c_k[/math] ごとに,クラスター [math]c_i[/math] に割り当てられたデータの平均を求め,それを [math]c_i[/math] の中心とする.
- 各データ [math]\bf{x}_1, \dots, \bf{x}_n[/math] に対して,データ [math]\bf{x}_i[/math] と各クラスター [math]c_1, \dots, c_k[/math] の中心との距離を求め,[math]\bf{x}_i[/math] を最も中心が近いクラスターに割り当て直す.
- 全てのデータについてクラスターの割り当てが変更されなかったら終了する.そうでない場合は,ステップ2へ戻る.
Rで[math]k[/math]平均法を用いるには,kmeans関数を用います. kmeans関数の引数には,分割するデータとクラスター数 [math]k[/math] を与えます.
model <- kmeans(data1, 2)
作成されたオブジェクトのcluster変数には割り当てられたクラスター番号が,center変数には各クラスターの中心座標が格納されます.
model$cluster
結果をプロットすると次のようになります.
> model$cluster [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [26] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [51] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [76] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [101] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 [126] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 [151] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 [176] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[math]k[/math]平均法の結果は,最初に行われるランダムな割り当てに依存します. nstartオプションの値(デフォルトは1)を2以上にすると,nstart回実行して最もよい結果を返します.
model$center
また,[math]k[/math]平均法を実行するたびに結果が変わるので,同じ結果を得るには,set.seed関数を用いて乱数のシードをセットしてから実行します.
> model$center x y 1 -0.9638605 -1.010867 2 1.0271218 0.967736
k平均法が苦手な問題 †
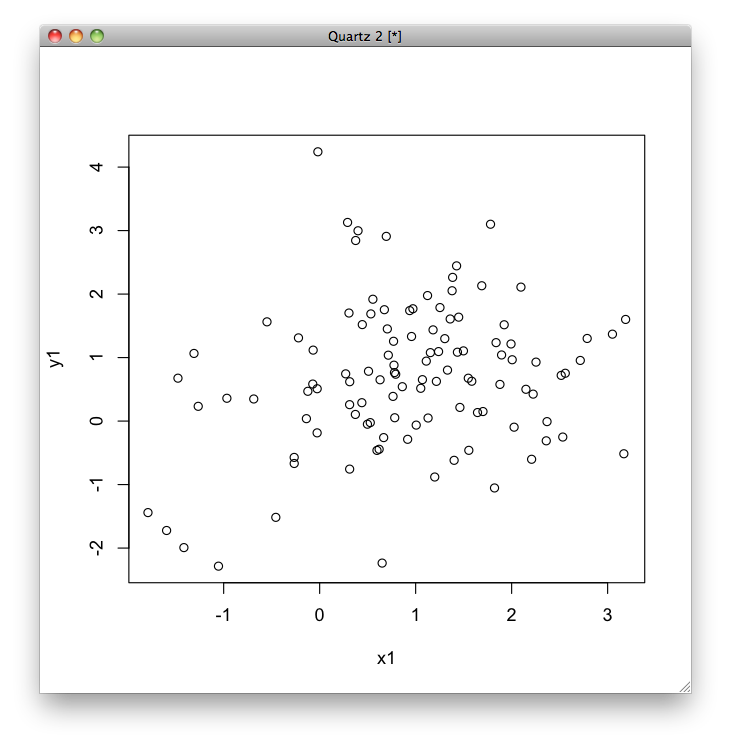
今度は,もう少し分散を大きくし,かつ,データの個数を同じにしないでやってみます.
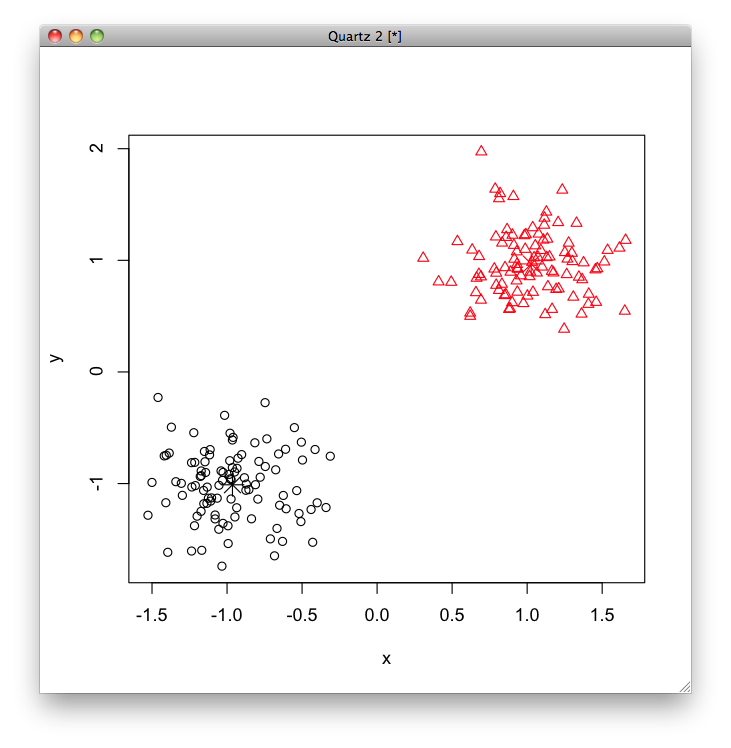
plot(data1, col=model$cluster, pch=model$cluster) points(model$centers, col=1:2, pch=8, cex=2)
> model <- kmeans(data1, 2, nstart=10)
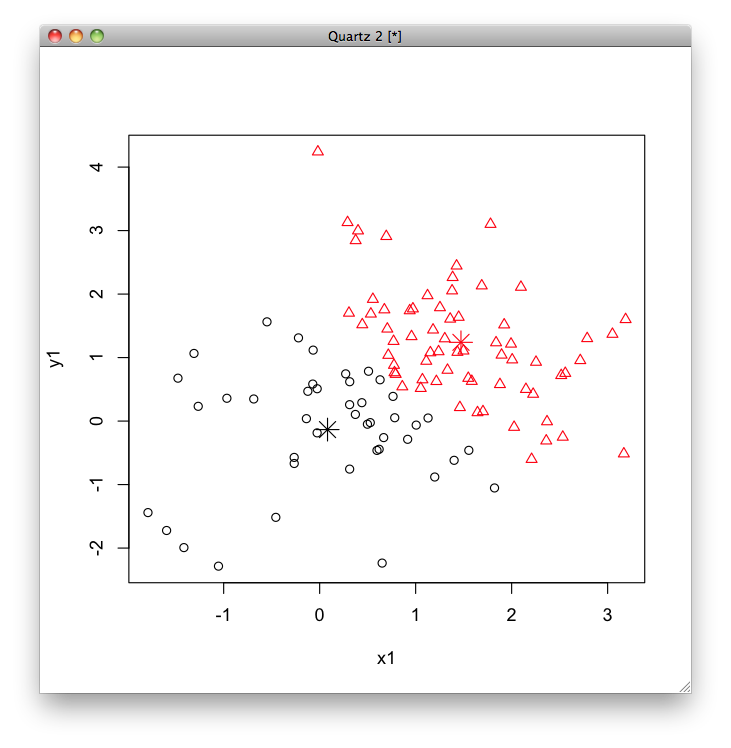
すると,データを生成するときに使用した中心 [math](1, 1), (-1, -1)[/math] よりもずれてしまいました. [math]k[/math]平均法はこういう問題はうまくクラスタリングできません.
irisデータセット †
irisデータセットでもやってみましょう.
set.seed(0) model <- kmeans(data1, 2)
このデータセットは,アヤメの種類(Species)をがく片の長さ(Sepal.Length),幅(Lepal.Width),花びらの長さ(Petal.Length),幅(Petal.Width)によって分類する問題です. 長さと幅は連続値,種類はsetosa, versicolor, virginicaのいずれかをとる離散値です.
このデータセットには,setosa, versicolor, virginicaという3種類のアヤメについて,それぞれ50個ずつ,合計150個のデータが含まれています. ランダムに10個のデータを選択して,見てみましょう.
set.seed(123) x1 = rnorm(100, mean=1, sd=1) y1 = rnorm(100, mean=1, sd=1) c1 <- cbind(x1, y1) x2 = rnorm(10, mean=-1, sd=1) y2 = rnorm(10, mean=-1, sd=1) c2 <- cbind(x2, y2) data2 <- rbind(c1, c2) plot(data2)
ここでは,Speciesを除いた1列目から4列目だけを取り出して使います.
model <- kmeans(data2, 2) plot(data2, col=model$cluster, pch=model$cluster) points(model$centers, col=1:2, pch=8, cex=2)
4次元データですが,このうちのSepal.LengthとPetal.Lengthだけを取り出して表示します. データを表示するときの色colと形pchにはirisのSpeciesをas.numeric関数で数値化したものを指定します.
data(iris)
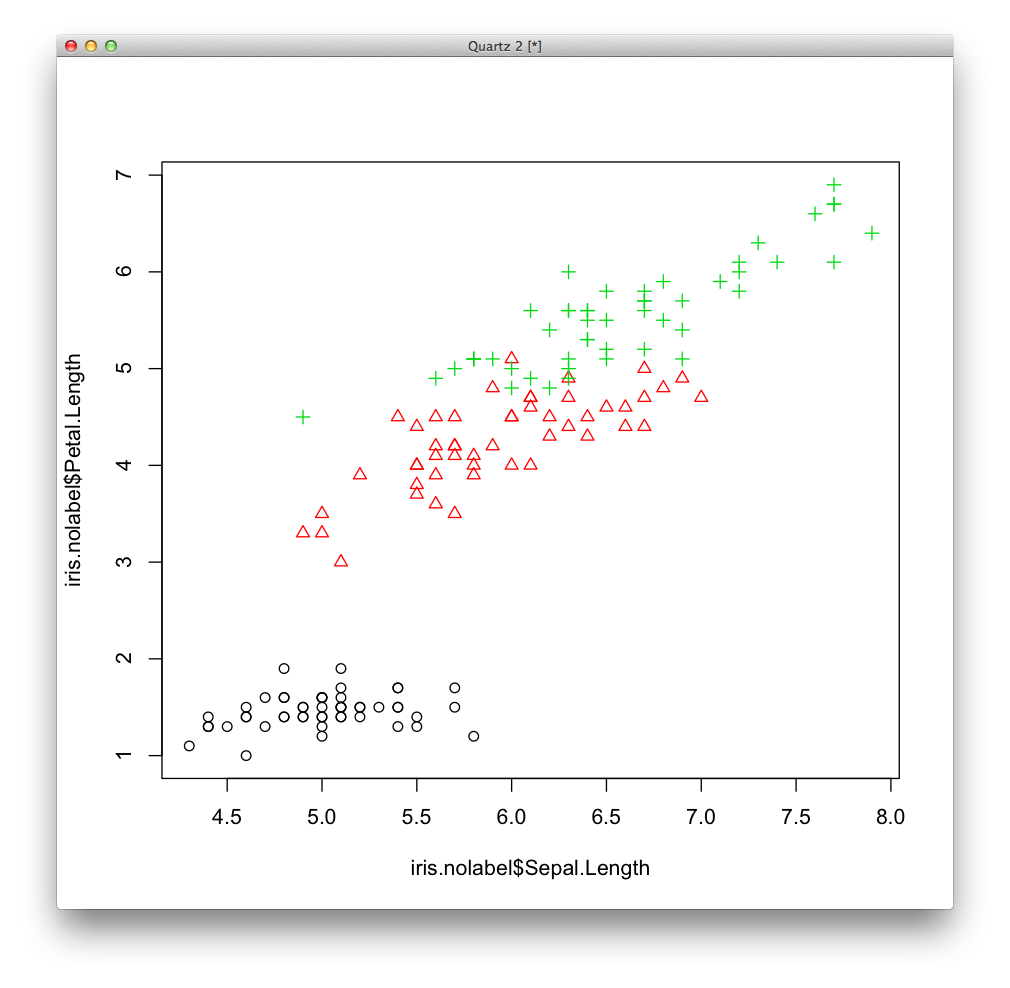
カテゴリーの数は3だとわかっていますので,[math]k=3[/math] として[math]k[/math]平均法によるクラスタリングを行います.
iris[sort(sample(1:150,10)),]
今度は色と形をクラスタリングによって得られたクラスター番号によって指定して表示します.
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
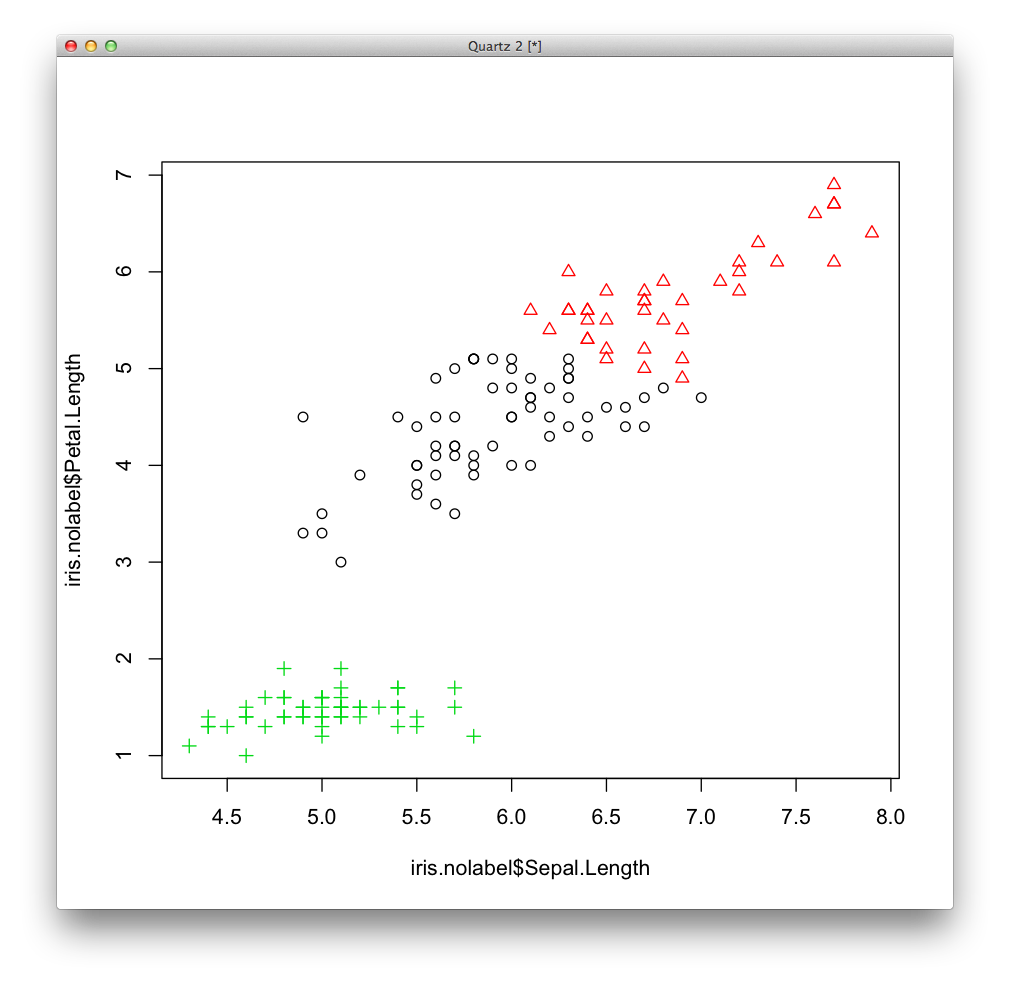
まとめ †
[math]k[/math]平均法は,[math]k[/math] 個のクラスターへの割り当てとクラスターの中心の計算を繰り返す,分割最適化アプローチのクラスタリング手法です.
[math]k[/math]平均法では,クラスターの数 [math]k[/math] をユーザーが事前に与えなければなりません. したがって,いくつかの [math]k[/math] を試して最もうまくいったものを採用するという方法をとることがあります.
[math]k[/math]平均法の結果は,最初に行われるランダムな割り当てに依存します. nstartオプションで複数回実行して最も良い結果を採用するか,乱数のシードを変えて実行すると,よりよい結果が得られる可能性があります.
また,[math]k[/math]平均法ではうまくいかない問題があることがよく知られています. そのようなときは,スペクトラル・クラスタリングを用いるとうまくいくかもしれません.
参考文献 †
- クラスタリングとは(クラスター分析とは) - 神嶌敏弘さん
- Rでスペクトラル・クラスタリングを使う - とうごろうぃき
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)