![[PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png "[PukiWiki]")
- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rで独立成分分析する へ行く。
この記事はまだ書きかけです．
はじめに †
ここでは，Rを使って独立成分分析を行います．
準備 †
Rのインストールについては，次のページを見てください．
独立成分分析は，fastICAパッケージに含まれています． そこで，fastICAパッケージをインストールします． install.packagesコマンドを実行すると，パッケージをダウンロードするサーバーを聞かれますので，リストからJapanのどれかを選択します．
> install.packages("fastICA") > library(fastICA)
独立成分分析 †
独立成分分析 (Independent Component Analysis, ICA) は，多変量解析の一手法で，高次元の数値データを（独立に生起している）複数の成分に分解する手法です．
複数の人が同時に話をすると，音声信号が混ざってしまいます． これを複数のマイクで拾って，元の成分に分解するのによく使われています．
[math]n[/math] 個の信号源から発生し（て混ざっ）た信号 [math]s_1, \dots, s_n[/math] を [math]m[/math] 個のセンサーで観測し [math]x_1, \dots, x_m[/math] を得たとします．
独立成分分析は，観測した [math]m[/math] 個のデータ [math] x_1, \dots, x_m[/math] から [math]n[/math] 個の（独立な）信号源から発生した [math]n[/math] 個のデータ [math]s_1, \dots, s_n[/math] に復元します．
これを信号行列 [math]S[/math] に対して，混合行列 [math]A[/math] が掛け合わされて観測行列 [math]X[/math] になった，つまり [math]X = AS[/math] と表し，独立成分分析では [math]X[/math] から [math]A[/math] を推定します．
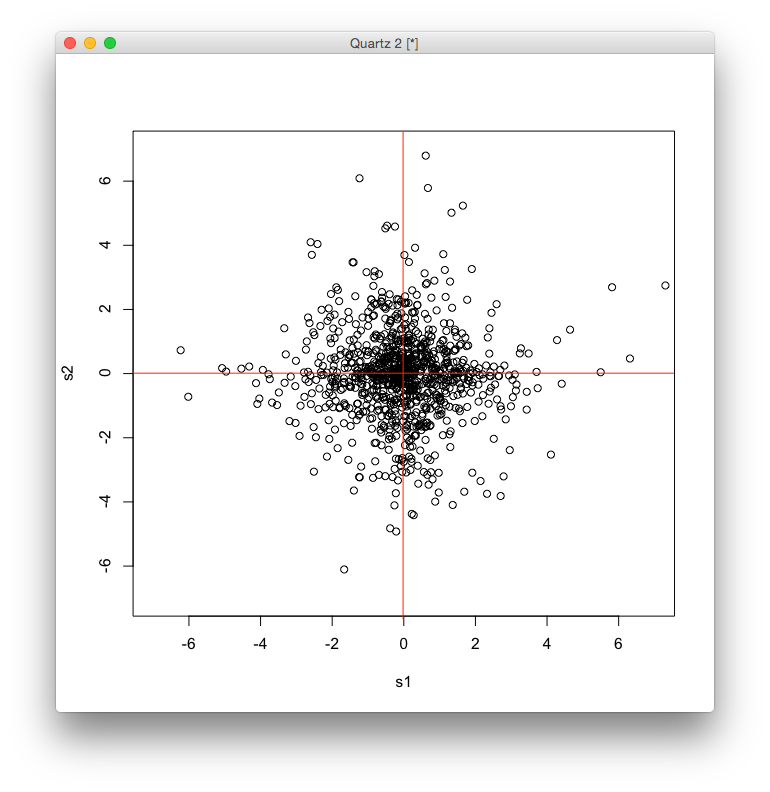
例として，2つの信号源（音源）からそれぞれ次のような信号（音） [math]s_1[/math] と [math]s_2[/math] が発生しているとします．
二つの信号源からちょうど同じ距離の地点でこの信号を観測すると，この信号が1:1の割合で混ざって観測されます． \[ x_1 = 0.5 s_1 + 0.5 s_2 \]
また，二つの信号源からの距離が4:1の地点でこの信号を観測すると，次のようになります． \[ x_2 = 0.4 s_1 + 0.1 s_2 \]
このような条件を満たす地点は二つの信号源を結ぶ直線と直行する直線上に無数に存在し，係数の大きさは信号源からどのくらい離れているかに比例します． ここでは，上のような係数だとします．
このとき，真の混合行列は以下のように表されます． \[ A = \begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.1 \end{bmatrix} \]
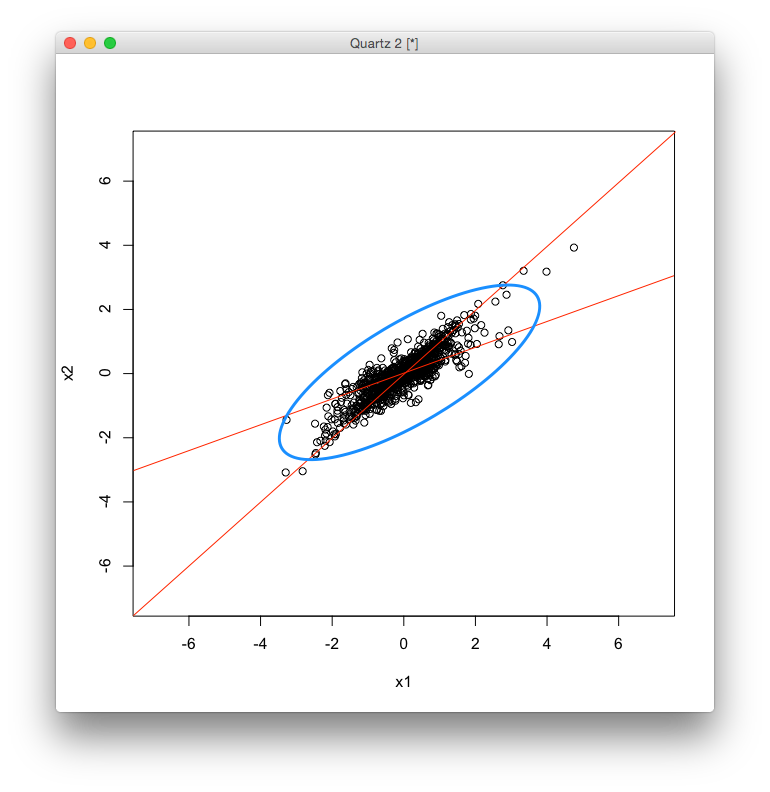
上の図の信号をこのようにして観測すると，次のような信号が得られます．
観測した [math]x_1[/math], [math]x_2[/math] の相関行列を求めると次のようになりました． \[ \begin{bmatrix} -0.08 & -0.12 \\ 0.12 & 0.06 \end{bmatrix} \]
これを単位行列に変換する処理を白色化といいます． [math]x_1[/math], [math]x_2[/math] を白色化した後の座標をそれぞれ [math]z_1[/math], [math]z_2[/math] とすると，相関行列を単位行列になっているので，[math]z_1[/math] と [math]z_2[/math] の相関がなくなっていて，それぞれの分散（標準偏差）が1に正規化されます．
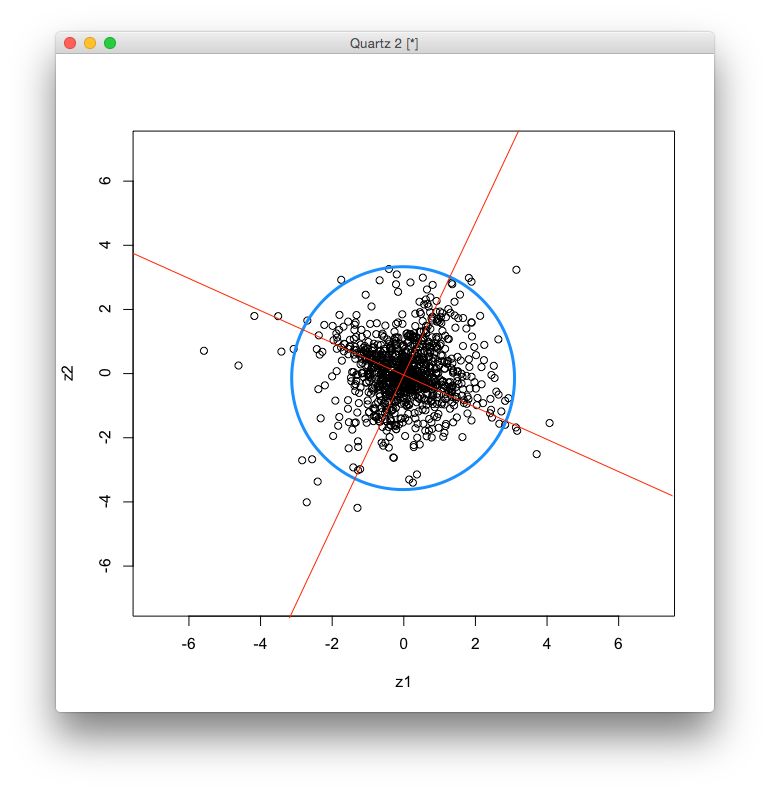
上の観測データを白色化すると次のようになります．
最後に，白色化したデータを2つの変数がもっとも独立となるように原点で回転させます．
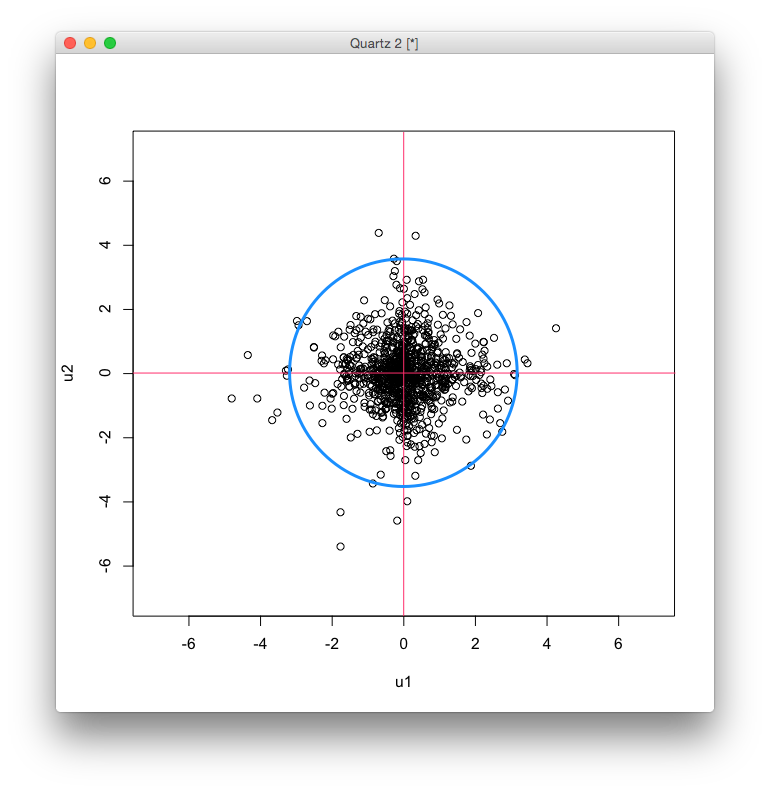
上の白色化したデータを2つの変数がもっとも独立となるように原点で回転させると，次のようになります．
このようにして推定された変換行列は次のようになりました． \[ \hat{A} = \begin{bmatrix} -0.52 & -0.10 \\ -0.72 & -0.70 \end{bmatrix} \]
求められた [math]u_1[/math] は [math]x_2[/math] に，[math]u_2[/math] は [math]s_1[/math] に対応しています．
独立成分分析では，独立性だけを考慮していますので，求められた成分に順序はありません． また，成分の向きとスケールは元の信号と一致しません． （向きは1/2の確率で偶然に一致します．）
独立成分分析を行う †
標準で使えるirisデータセットに対して，独立成分分析を行ってみましょう．
> data(iris)
このデータセットは，アヤメの種類 (Species) を花びらの長さ (Sepal.Length)，幅 (Lepal.Width)，がくの長さ (Petal.Length)，幅 (Petal.Width) によって分類する問題です． 長さと幅は連続値，種類はsetosa, versicolor, virginicaのいずれかをとる離散値です．
このデータセットには，setosa, versicolor, virginicaという3種類のアヤメについて，それぞれ50個ずつ，合計150個のデータが含まれています． ランダムに10個のデータを選択して，見てみましょう．
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
このデータは，1つの信号源からの信号 (Species) を4つのセンサーで観測してSepal.Length, Sepal.Width, Petal.Length, Petal.Widthを得たものと考えることができます．
Rで独立成分分析を行うには，fastICAパッケージのfastICA関数を用います． 引数にはデータと信号源の数を与えます．
> iris.ic <- fastICA(iris[1:4], 4)
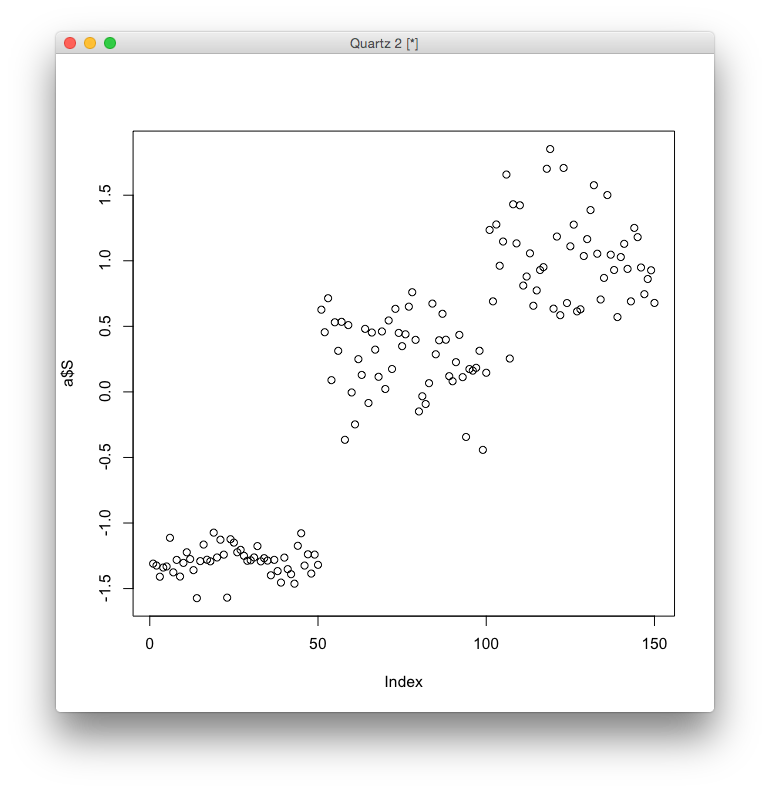
得られたオブジェクトの変数 S に推定された源信号が格納されています．
> pairs(iris.ic$S, pch=as.integer(iris$Species))
得られたオブジェクトの変数 A に推定された混合行列が格納されています．
> iris.ic$A [,1] [,2] [,3] [,4] [1,] 0.21328403 0.37157377 0.09047249 0.05272770 [2,] -0.67224217 0.20889006 -1.74869766 -0.73629270 [3,] 0.06631234 -0.06327993 0.06929867 -0.17430924 [4,] 0.42346817 0.05483076 0.15675322 0.04291885
