- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rで決定木を使う へ行く。
はじめに †
『Rによるバイオインフォマティクスデータ解析』の7.13節「決定木」を参考にして,決定木を学習します.
準備 †
Rのインストールと基本的な使い方については,次のページを見てください.
最初は,標準で使用できるirisデータセットを使います.
data(iris)
このデータセットは,アヤメの種類(Species)をがく片の長さ(Sepal.Length),幅(Lepal.Width),花びらの長さ(Petal.Length),幅(Petal.Width)によって分類する問題です. 長さと幅は連続値,種類はsetosa, versicolor, virginicaのいずれかをとる離散値です.
このデータセットには,150個のデータが含まれています. ランダムに10個のデータを選択して,見てみましょう.
iris[sort(sample(1:150,10)),]
ここでは,treeパッケージ*1*2を使います. install.packagesコマンドを入力すると,パッケージをダウンロードするサーバーを聞かれますので,リストからJapanを選択します.
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
決定木を学習する †
決定木学習は,説明変数に対する条件を用いて事例集合を分割することによってラベル(カテゴリー)を予測するための決定木を学習するものです. 実物を見た方が理解しやすいので早速決定木を学習します.
まず,treeコマンドを用いて決定木を学習します.
install.packages("tree") library(tree)
ここで,第1引数の「Species ~ .」はモデル式,第2引数の「iris」は訓練データを表しています. モデル式は「目的変数 ~ 説明変数」という形で表現し,説明変数が「.」(ドット)のときは,目的変数以外の全ての変数を表します. したがって,ここでは,irisデータセットのSpeciesを目的変数とし,それ以外のすべての変数(Spepal.Lenght, Sepal.Width, Petal.Length, Petal.Width)を説明変数としています.
次に,学習された決定木を表示します.
model <- tree(Species~., iris)
テキストでは分かりにくいので,図にします.
model

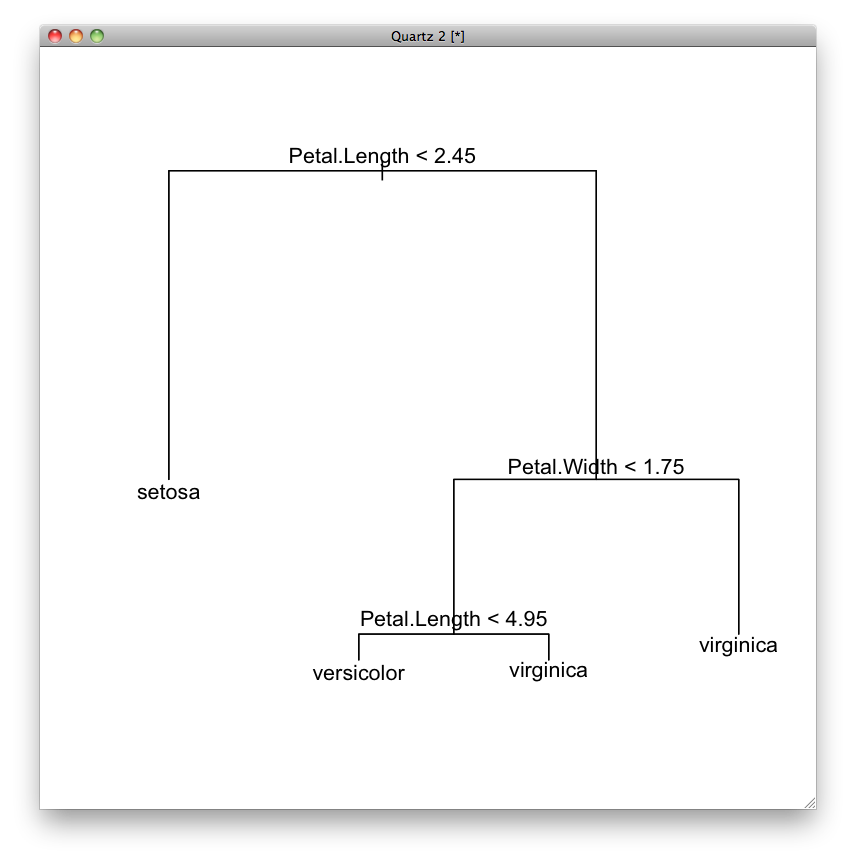
一番上が根(root)と呼ばれます. 根から枝(branch)が下へと伸び,節(node)で分岐します. 節は条件に対応します. 枝の先端が葉(leaf)で,葉はカテゴリー(ラベル)に対応します.
最初に,根の条件「Petal.Lengthの値が2.45より小さいか」によって事例を分けます. Petal.Lengthの値が2.45よりも小さい事例は左に,そうでない事例は右に振り分けられます. 右に振り分けられた事例は,次に,2番目の条件「Petal.Widthの値が1.75より小さいか」によって振り分けられます. Petal.Widthの値が1.75よりも小さい事例は左に,そうでない事例は右に振り分けられます.
ここで右に振り分けられた事例は,「Petal.Lengthの値が2.45より大きい」かつ「Petal.Widthの値が1.74より大きい」事例です. このように,決定木は,論理積(かつ)で結合した条件を表しています.
先に表示したテキストで見てみましょう.
最初の条件で分割する前の集合は 1) です. 最初のrootのところは条件を表しますが,ここでは条件がないのでrootと書かれています. 150はこの集合に含まれる事例の数,239.600はこの集合に含まれる事例のバラツキの度合いです. そしてsetosaはこの集合に振り分けられた事例に対する予測ラベルです. ( 0.33333 0.33333 0.33333 )は,setosa, versicolor, virginicaの出現確率を表しています.
最初の条件は「Petal.Length < 2.45」です. この条件に当てはまる事例の集合が 2) で,そうでない事例の集合が 3) です. このような分割が葉に至るまで続きます.
ここで,図の右下の条件を見ると,「Petal.Length < 4.95」という条件で分割していますが,どちらに振り分けられてもvirginicaと予測されています. 同じように,左下の条件でも左右ともversicolorになっています. 前者の集合は 7),後者の集合は 12) です.
そこで,この条件を決定木から取り除きます. これを枝刈りといいます. 枝刈りをするには,snip.tree関数を使って,nodeオプションに枝刈りする(条件分岐を止める)節番号のベクトルを指定します.
> model node), split, n, deviance, yval, (yprob) * denotes terminal node 1) root 150 329.600 setosa ( 0.33333 0.33333 0.33333 ) 2) Petal.Length < 2.45 50 0.000 setosa ( 1.00000 0.00000 0.00000 ) * 3) Petal.Length > 2.45 100 138.600 versicolor ( 0.00000 0.50000 0.50000 ) 6) Petal.Width < 1.75 54 33.320 versicolor ( 0.00000 0.90741 0.09259 ) 12) Petal.Length < 4.95 48 9.721 versicolor ( 0.00000 0.97917 0.02083 ) 24) Sepal.Length < 5.15 5 5.004 versicolor ( 0.00000 0.80000 0.20000 ) * 25) Sepal.Length > 5.15 43 0.000 versicolor ( 0.00000 1.00000 0.00000 ) * 13) Petal.Length > 4.95 6 7.638 virginica ( 0.00000 0.33333 0.66667 ) * 7) Petal.Width > 1.75 46 9.635 virginica ( 0.00000 0.02174 0.97826 ) 14) Petal.Length < 4.95 6 5.407 virginica ( 0.00000 0.16667 0.83333 ) * 15) Petal.Length > 4.95 40 0.000 virginica ( 0.00000 0.00000 1.00000 ) *
plot(model) text(model)
これで完成です.
テスト・データのカテゴリーを予測する. †
学習した決定木を使って,カテゴリー(Species)が未知のデータに対してそのカテゴリーを予測してみましょう.
まず,data.frame関数を用いてデータ・フレームを作成します.
snip <- snip.tree(model, nodes=c(7,12)) plot(snip) text(snip)
次に,predict関数を用いてカテゴリーを予測します.
snip
1番目の事例はvirginicaに,2番目の事例はversicolorに,3番目の事例はsetosaと予測されました.
また,枝刈りされた決定木を用いて予測すると次のようになります.
> snip node), split, n, deviance, yval, (yprob) * denotes terminal node 1) root 150 329.600 setosa ( 0.33333 0.33333 0.33333 ) 2) Petal.Length < 2.45 50 0.000 setosa ( 1.00000 0.00000 0.00000 ) * 3) Petal.Length > 2.45 100 138.600 versicolor ( 0.00000 0.50000 0.50000 ) 6) Petal.Width < 1.75 54 33.320 versicolor ( 0.00000 0.90741 0.09259 ) 12) Petal.Length < 4.95 48 9.721 versicolor ( 0.00000 0.97917 0.02083 ) * 13) Petal.Length > 4.95 6 7.638 virginica ( 0.00000 0.33333 0.66667 ) * 7) Petal.Width > 1.75 46 9.635 virginica ( 0.00000 0.02174 0.97826 ) *
1番目の事例は97.8%の確率でvirginicaに,2.2%の確率でversicolorに分類されると予測されました. 同様に,2番目の事例は97.9%の確率でversicolorに,2.1%の確率でverginicaに分類されると予測されました. 3番目の事例は枝刈りしなかったときと同様に100%の確率でsetosaと予測されました.
まとめ †
決定木は,目的変数が離散値(カテゴリー値)のときに用いられる分類手法です.
決定木のrootからそれぞれの葉(ラベル)に到達するまでの条件を全て論理積(かつ)で結合したif-thenルールに変換することができます.
「学習されたルールがとてもわかりやすい」という点が特徴です.
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)