- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/RでSVMを使う へ行く。
このページはまだ書きかけです.
はじめに †
『Rによるバイオインフォマティクスデータ解析』の7.15「SVM」を参考にして,RでSVMを使って学習します.
準備 †
Rのインストールについては,次のページを見てください.
Naïve Bayesは,e1071パッケージに含まれています. そこで,e1071パッケージをインストールします. install.packagesコマンドを実行すると,パッケージをダウンロードするサーバーを聞かれますので,リストからJapanのどれかを選択します.
install.packages("e1071") library("e1071")
ここでは,標準で使用できるirisデータセットを使います.
data(iris)
このデータセットは,アヤメの種類(Species)を花びらの長さ(Sepal.Length),幅(Lepal.Width),がくの長さ(Petal.Length),幅(Petal.Width)によって分類する問題です. 長さと幅は連続値,種類はsetosa, versicolor, virginicaのいずれかをとる離散値です.
このデータセットには,setosa, versicolor, virginicaという3種類のアヤメについて,それぞれ50個ずつ,合計150個のデータが含まれています. ランダムに10個のデータを選択して,見てみましょう.
iris[sort(sample(1:150,10)),]
これをランダム・サンプリングして80%を訓練データとし,のこりの20%をテスト・データとします.
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
SVM †
SVM(サポート・ベクター・マシン)は二値分類を行う教師付き学習の手法で,高い汎化能力を持っています.
SVMが高い汎化能力を持つ理由の一つが,カーネル・トリックというテクニックが使えることです. これは,元の空間で線形分離が不可能なときでも,カーネルと呼ばれる写像関数を用いて,線形分離可能な空間にマッピングすることで,線形分離を可能にするというものです.
SVMは,最初,二値分類用に開発されましたが,その語,同じ技術を使って回帰を行う手法が開発されました. そこで,最近では,分類用のSVMをSVC(サポート・ベクター分類),回帰用のSVMをSVR(サポート・ベクター回帰)と呼んで区別します.
ここでは,分類用のSVM,つまりSVCのことを単にSVMと呼びます.
SVMは,高次元空間の中で,正事例と負事例を分離する超平面(線形判別関数)を求めます. したがって,説明変数はすべて実数値でなければなりません.
分離超平面から最も近い事例をサポート・ベクターといい,分離超平面からサポート・ベクターまでの間の部分をマージンと呼びます.
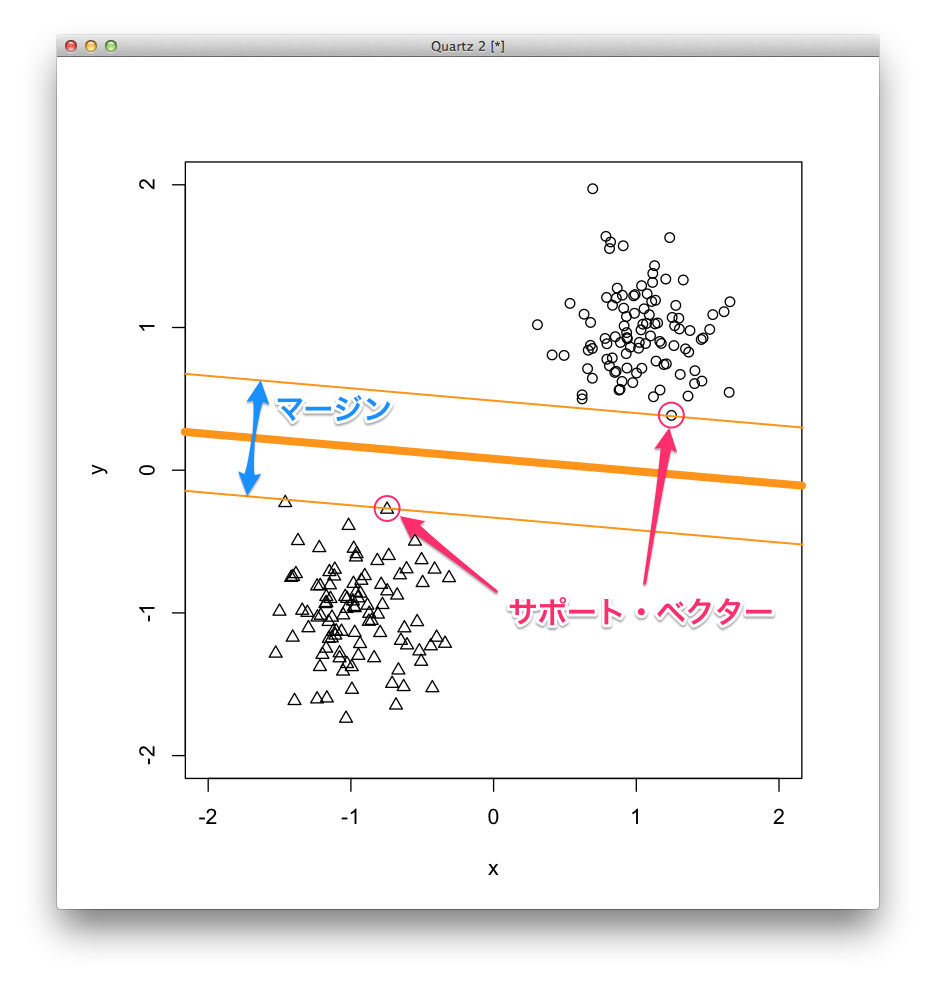
SVMは,このマージンが最も大きい分離超平面を求めます. これをマージン最大化といいます.
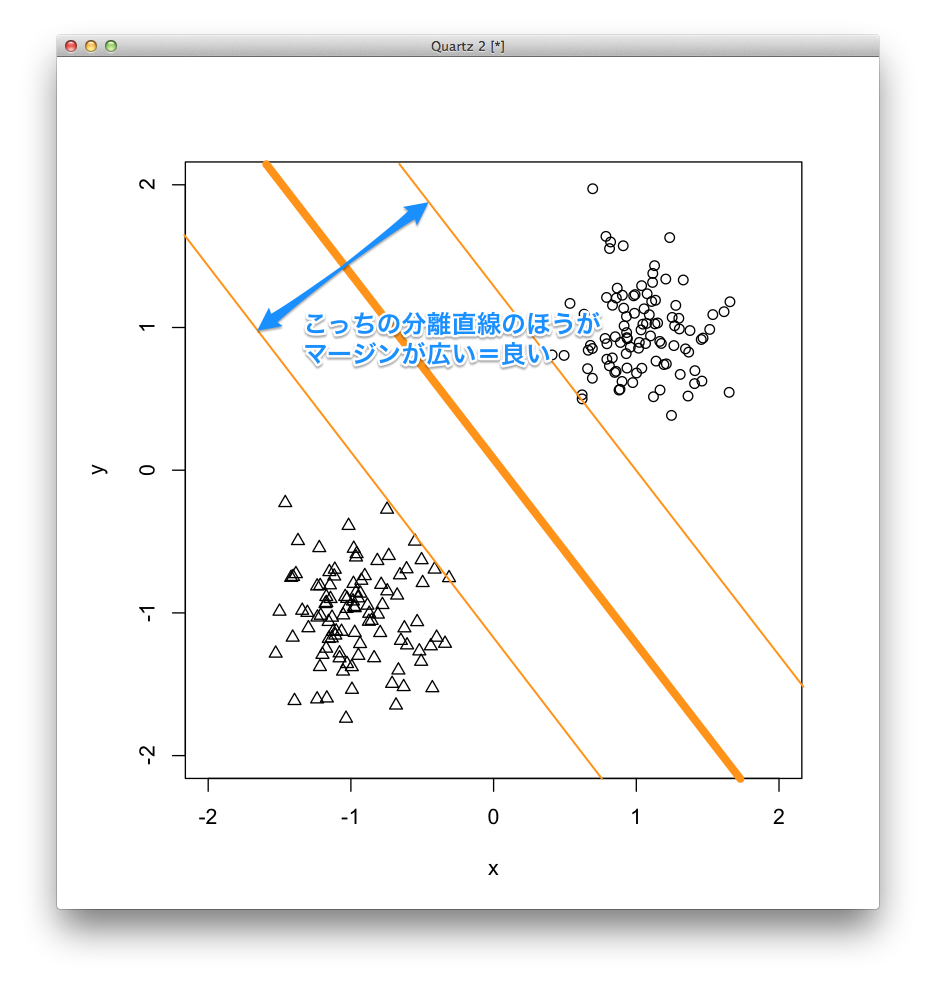
分離超平面で正事例と負事例を完全に分けられるならこれで良いのですが,どうしても分けられない場合もあります. 分けられると仮定するSVMをハード・マージンSVMといい,分けられないときのためのSVMをソフト・マージンSVMといいます.
ソフト・マージンSVMでは,マージンの内側からはみ出している事例に対してペナルティを与え,このペナルティをスラック変数 [math]\xi[/math] で表します. マージンの内側からはみ出していない事例のスラック変数の値はゼロ,つまり,ペナルティなしです.
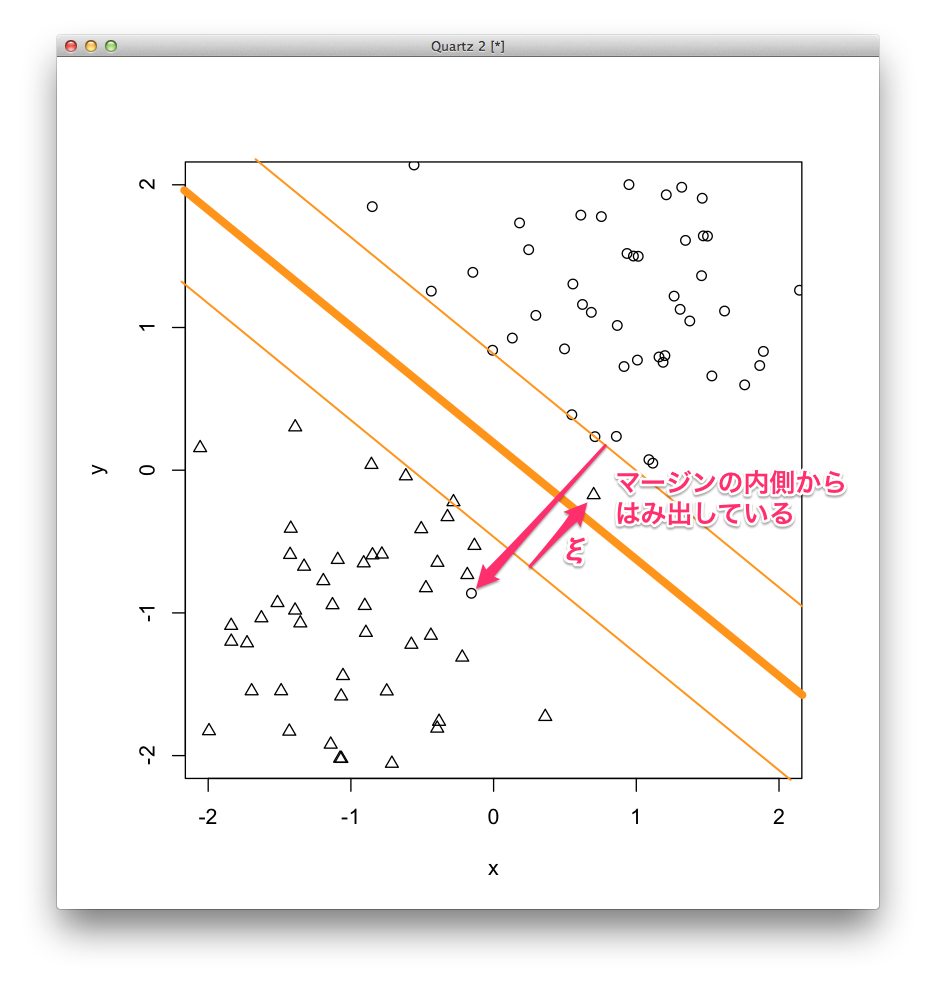
ここからはソフト・マージンSVMのことを単にSVMと呼びます.
SVMの判別関数は次の式で表されます. \[ f(\mathbf{x}) = \mathbf{x}^\mathrm{T} \mathbf{w} + b \] ここで,[math]\mathbf{x}[/math] は説明変数ベクトル,[math]\mathbf{w}[/math] は係数ベクトル,[math]b[/math] は切片を表します. つまり,判別関数を説明変数 [math]x_1[/math], [math]x_2[/math], ..., [math]x_p[/math] の線形和とし,各説明変数の係数 [math]w_1[/math], [math]w_2[/math], ..., [math]w_p[/math] と切片 [math]b[/math] を学習します.
SVMは次のような [math]\mathbf{w}[/math] と [math]b[/math] を求めます. \[ \mathrm{argmin}_{\mathbf{w}, b} C \sum_1^n \xi_i + \frac{1}{2} ||\mathbf{w}||^2 \]
[math]\sum_1^n \xi_i[/math] はスラック変数の総和,つまり,ペナルティの総和です. これを最小化するということは,ペナルティの総和が小さいほどいいという意味になります.
[math]||\mathbf{w}||^2[/math] は正則化項です. これを最小化するということは,係数の絶対値は小さいほどいいという意味になります.
[math]C[/math] はペナルティの総和と正則化項のどちらをどのくらい重視するかを表すパラメーターです.
SVMの実行 †
e1071パッケージのSVMを使うには,svm関数を用います. svm関数の引数には,モデル式と訓練データを与えます.
idx <- sample(nrow(iris), as.integer(nrow(iris)*0.8)) iris.train <- iris[idx,] iris.test <- iris[-idx,]
モデル式は,「目的変数 ~ 説明変数」という形をしていて,複数の説明変数を指定するときは記号 +(プラス)で連結します. また,この例のように,目的変数以外全部を説明変数とするときは,記号 .(ドット)で表すことができます.
irisデータのSpeciesにはsetosa, versicolor, virginicaという3つの値があるので,2値分類であるSVMはそのまま適用することはできませんが,setosaとその他,versicolorとその他,virginicaとその他というように,2値分類を3回行ってその結果を総合して多値分類を行っています.
学習したモデルを表示すると次のようになります.
model <- svm(Species~., data=iris.train)
SVM-TypeはSVMの種類を表し,C-classificationというのは,上で説明したパラメーター [math]C[/math] を調整するタイプのSVCです. C-SVCともいいます.
SVM-Kernelはカーネル・トリックに用いられたカーネル(マッピング)の種類を表し,radialは動径基底関数(RBF, radial basis function)を用いたカーネルです. RBFカーネル, ガウシアン・カーネルともいいます.
costはC-SVCのパラメーター [math]C[/math],gammaはRBFカーネルのパラメーターです.
そして一番下にはサポート・ベクターの数が出ています.
テスト・データの予測 †
SVMで学習したモデルを用いてテスト・データに対してカテゴリーを予測してみましょう.
予測するには,predict関数を使います. predicrt関数には,学習したモデルとテスト・データを引数として与えます.
model
予測結果と正解ラベルを突き合わせて表を作ります.
> model Call: svm(formula = Species ~ ., data = iris.train) Parameters: SVM-Type: C-classification SVM-Kernel: radial cost: 1 gamma: 0.25 Number of Support Vectors: 49
このページはまだ書きかけです.
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)