- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rで主成分分析する へ行く。
このページはまだ書きかけです
はじめに †
準備 †
データ
> data(iris)
主成分分析 †
主成分分析は,多変量解析の一手法で,高次元の数値データに対して合成成分を作る手法です.
この合成成分のことを主成分といい,次のように表されます.
\[\begin{array}{c@{}c@{}c} z_1&=&a_{1,1} x_{1} + a_{1,2} x_{2} + \dots + a_{1,p} x_{p} \\z_2 &=& \end{array}\]
例として,次のような2次元のデータを考えてみます.
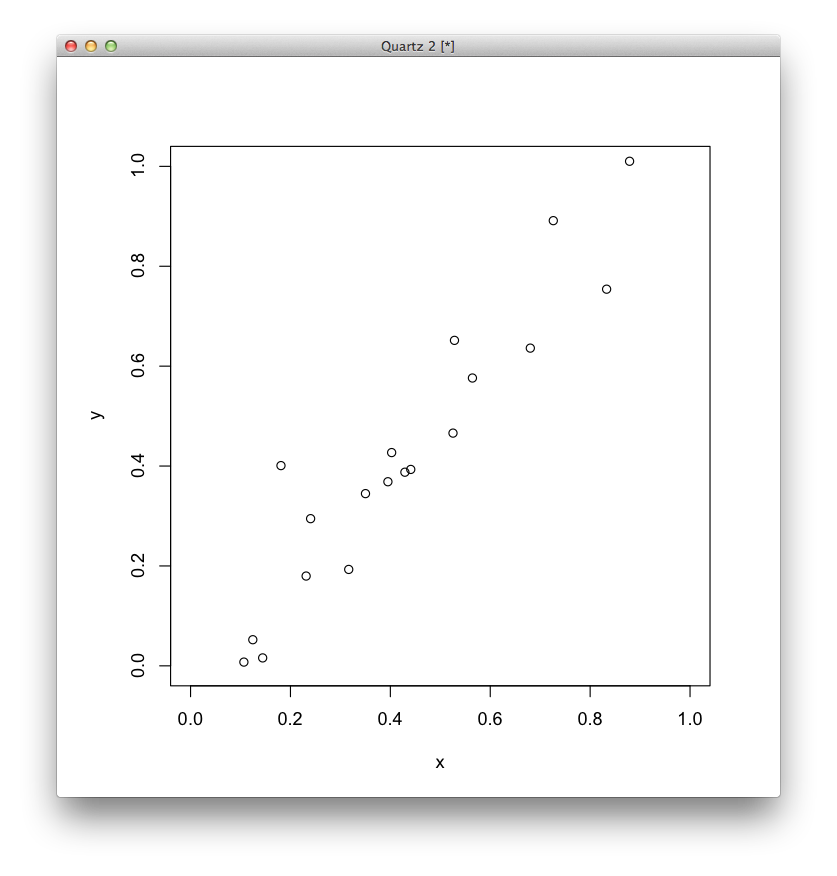
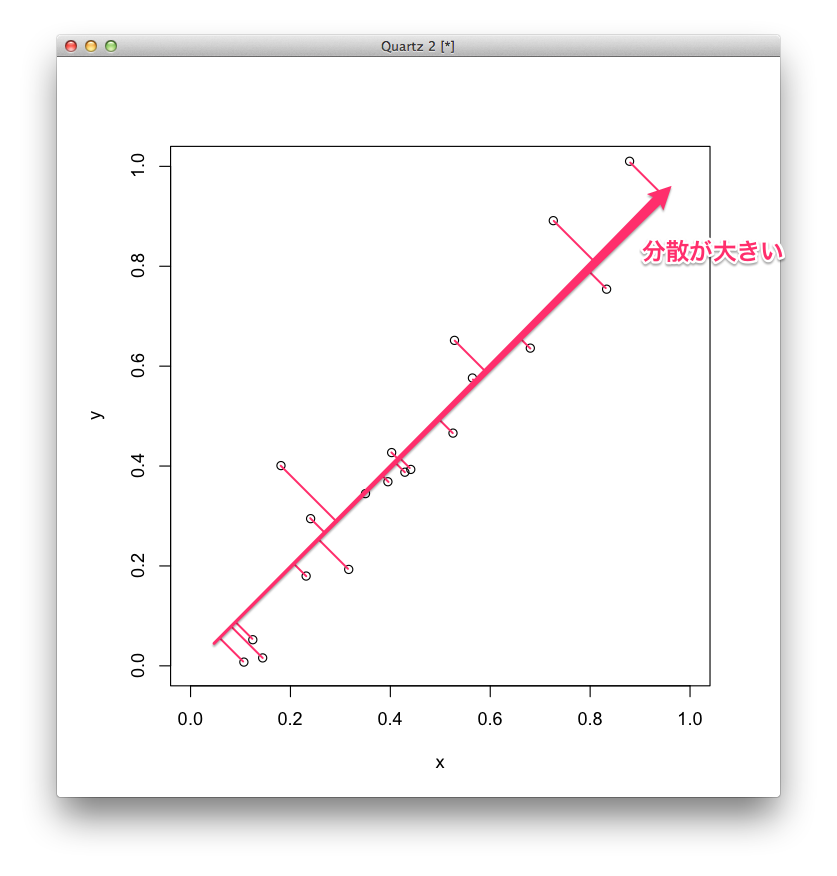
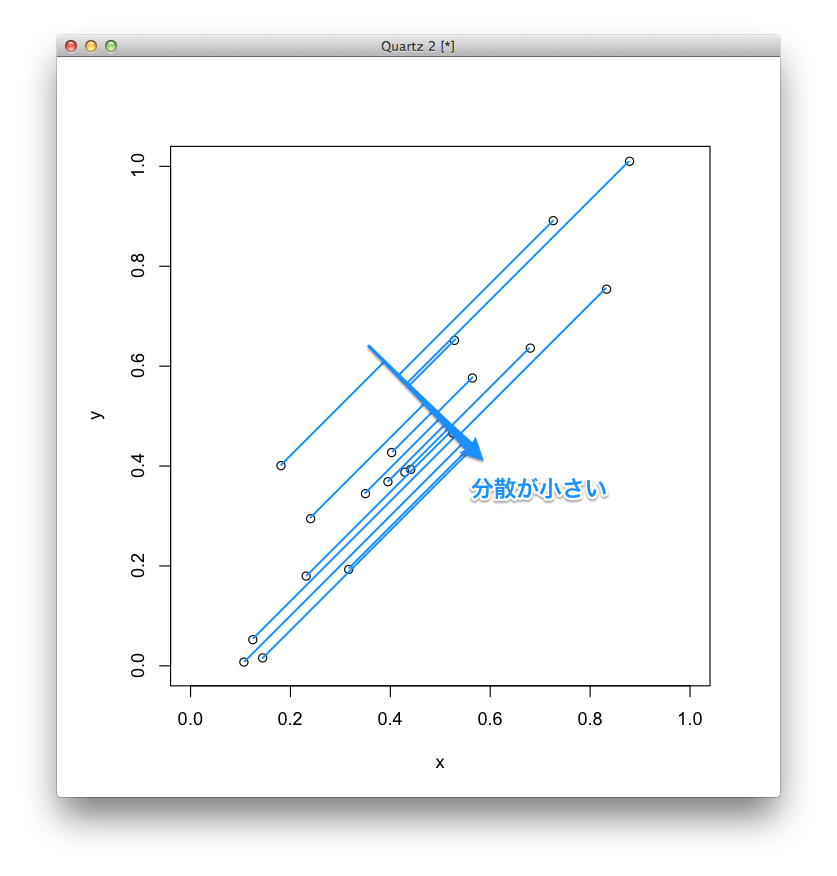
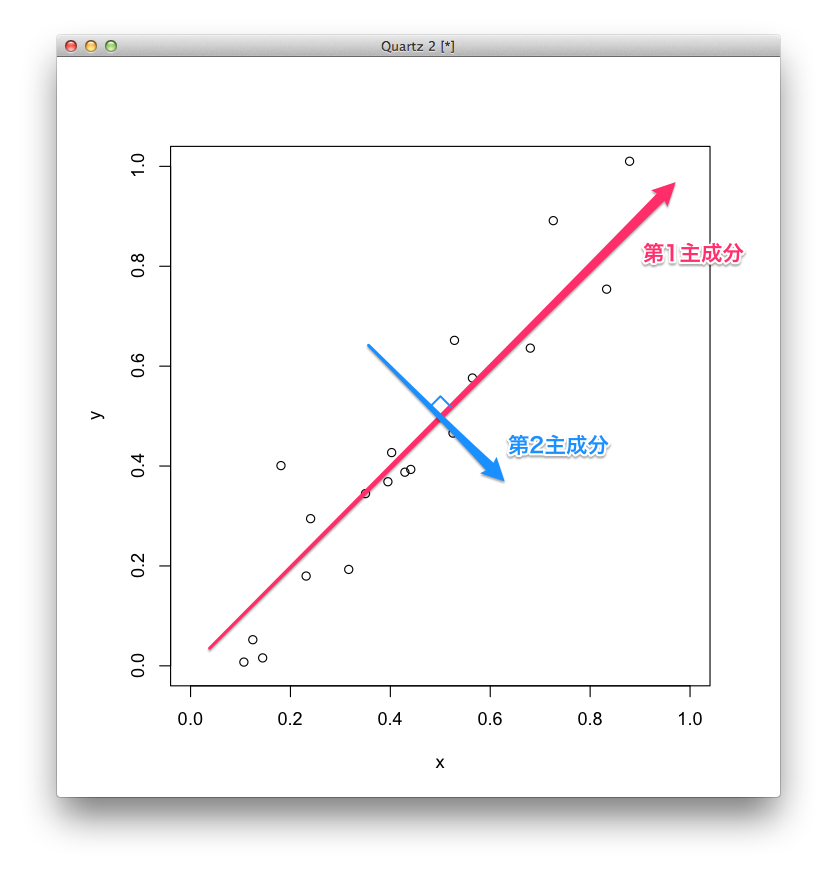
主成分分析を実行する †
主成分分析を実行
> iris[sort(sample(1:150,10)),] Sepal.Length Sepal.Width Petal.Length Petal.Width Species 4 4.6 3.1 1.5 0.2 setosa 22 5.1 3.7 1.5 0.4 setosa 65 5.6 2.9 3.6 1.3 versicolor 97 5.7 2.9 4.2 1.3 versicolor 100 5.7 2.8 4.1 1.3 versicolor 108 7.3 2.9 6.3 1.8 virginica 116 6.4 3.2 5.3 2.3 virginica 122 5.6 2.8 4.9 2.0 virginica 136 7.7 3.0 6.1 2.3 virginica 146 6.7 3.0 5.2 2.3 virginica
主成分分析の結果
> model <- princomp(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width, data=iris, cor=T)
固有ベクトル
> model Call: princomp(formula = ~Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, data = iris, cor = T) Standard deviations: Comp.1 Comp.2 Comp.3 Comp.4 1.7083611 0.9560494 0.3830886 0.1439265 4 variables and 150 observations. > summary(model) Importance of components: Comp.1 Comp.2 Comp.3 Comp.4 Standard deviation 1.7083611 0.9560494 0.38308860 0.143926497 Proportion of Variance 0.7296245 0.2285076 0.03668922 0.005178709 Cumulative Proportion 0.7296245 0.9581321 0.99482129 1.000000000
固有値
> unclass(model$loadings) Comp.1 Comp.2 Comp.3 Comp.4 Sepal.Length 0.5210659 -0.37741762 0.7195664 0.2612863 Sepal.Width -0.2693474 -0.92329566 -0.2443818 -0.1235096 Petal.Length 0.5804131 -0.02449161 -0.1421264 -0.8014492 Petal.Width 0.5648565 -0.06694199 -0.6342727 0.5235971
因子寄与率(主成分寄与率)
> model$sd^2 Comp.1 Comp.2 Comp.3 Comp.4 2.91849782 0.91403047 0.14675688 0.02071484
因子負荷量(主成分負荷量)
> model$scores Comp.1 Comp.2 Comp.3 Comp.4 1 -2.26470281 -0.480026597 0.127706022 0.024168204 2 -2.08096115 0.674133557 0.234608854 0.103006775 3 -2.36422905 0.341908024 -0.044201485 0.028377053 4 -2.29938422 0.597394508 -0.091290106 -0.065955560 5 -2.38984217 -0.646835383 -0.015738196 -0.035922813 ...
tは行列などを転置する関する,drop=F は行列と表示するオプション.
主成分分析の結果をグラフに表示する †
> biplot(model)
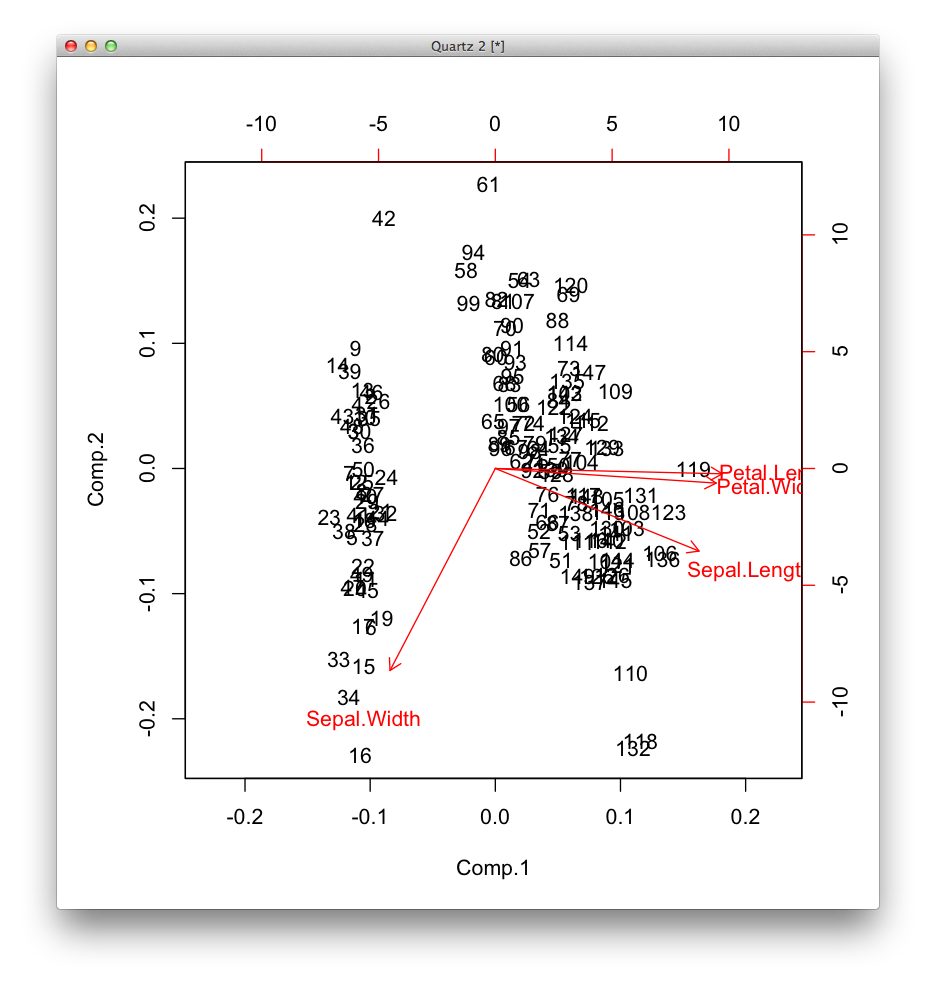
主成分スコアを求める †
データの行列と固有ベクトルの内積を求める
df <- data.frame(model$scores) df <- transform(df, Species=iris$Species) library(ggplot2) ggplot(data=df, aes(x=Comp.1, y=Comp.2, color=Species, shape=Species)) + geom_point() + theme(aspect.ratio=1)
%*% は行列の積.
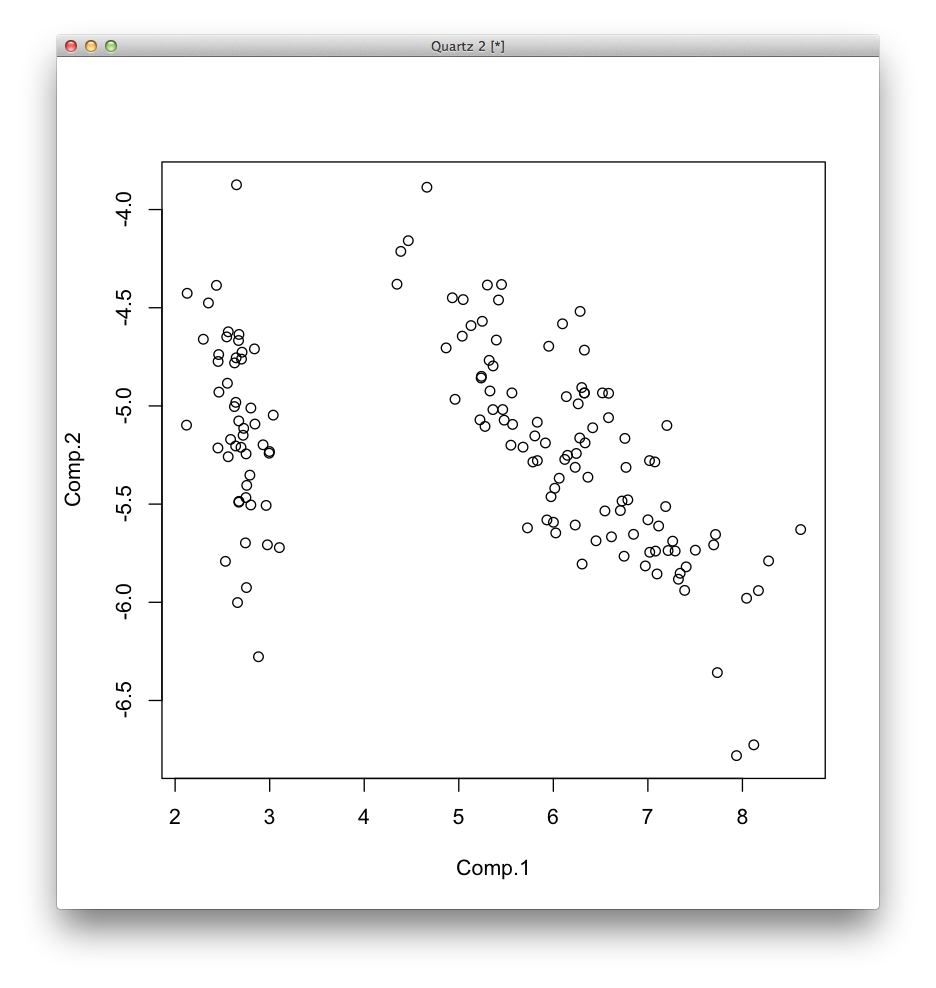
これをグラフにプロットする.
> plot(data.matrix(iris[,c(1,2,3,4)]) %*% unclass(loadings(iris.pc)[,c(1,2)]))
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)