- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- 機械学習/Pythonで決定木を使う へ行く。
- 1 (2017-08-21 (月) 13:16:16)
- 2 (2017-08-21 (月) 13:59:48)
- 3 (2017-08-22 (火) 00:46:39)
- 4 (2017-08-22 (火) 07:20:39)
- 5 (2017-08-22 (火) 11:50:16)
- 6 (2017-08-23 (水) 12:35:44)
- 7 (2017-08-25 (金) 13:49:18)
- 8 (2017-08-29 (火) 11:42:06)
- 9 (2017-09-06 (水) 20:05:52)
- 10 (2017-09-06 (水) 20:05:52)
- 11 (2017-09-06 (水) 20:05:52)
目次 †
はじめに †
ここでは、Pythonのデータ分析ライブラリーであるpandas、機械学習ライブラリーであるscikit-learn、実行環境であるJupyter Notebookを用いて、決定木による分類を行います。
分類とは、答えがある機械学習である教師付き機械学習のうち、答えがカテゴリー、ラベル、クラスと行った離散値であるもののことです。
scikit-learnに付属するデータを用いているサンプルはたくさんありますが、自分で実践するときは、データ・ファイルの読み込みからやらないといけません。 そこで、ここでは、DeepAnalyticsフォーマットのファイルを想定して、データ・ファイルの読み込みから予測結果の出力まで、一通りやります。
この内容は、以下の環境で確認しました。
- Python 3.5.1
- pandas 0.20.2
- NumPy 1.13.0
- scikit-learn 0.18.1
- Jupyter Notebook 5.0.0
- IPython 6.1.0
- Graphviz 2.36.0
- pydotplus 2.0.2
データ †
ここでは、irisデータをサンプルとして用います。
このデータセットは,アヤメの種類(class)を花びらの長さ(sepal length),幅(sepal width),がくの長さ(petal length),幅(petal width)によって分類する問題です. 長さと幅は連続値,種類はIris-setosa, Iris-versicolor, Iris-virginicaのいずれかをとる離散値です.
DeepAnalyticsのフォーマットに倣って、訓練データを train.tsv、テストデータを test_X.tsvとして、タブ区切りのCSVファイルで保存されているものとします。
今回のサンプルファイルはこれです。
train.tsv †
train.tsvはこんな感じです。
| id | sepal lentgh | sepal width | petal length | petal width | class |
| 2 | 4.9 | 3 | 1.4 | 0.2 | Iris-setosa |
| 52 | 6.4 | 3.2 | 4.5 | 1.5 | Iris-versicolor |
| 101 | 6.3 | 3.3 | 6 | 2.5 | Iris-virginica |
| ... | ... | ... | ... | ... | ... |
test_X.tsv †
test_X.tsvはこんな感じです。
| id | sepal length | sepal width | petal length | petal width |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 |
| 51 | 7 | 3.2 | 4.7 | 1.4 |
| 103 | 7.1 | 3 | 5.9 | 2.1 |
| ... | ... | ... | ... | ... |
データの読み込み †
pandasのread_csvを使って、タブ区切りのCSVファイルを読み込みます。 タブ区切りなので delimiter オプションを、先頭の列がインデックスなので index_col オプションを指定します。
import pandas as pd df_iris_train = pd.read_csv('train.tsv', delimiter='\t', index_col=0) df_iris_test = pd.read_csv('test_X.tsv', delimiter='\t', index_col=0)
読み込んだデータは、pandasのDataFrameとなります。 次のようにすると、Jupyter Notebook上でDataFrameを確認できます。
df_iris_train
df_iris_test
決定木の学習 †
決定木 (Decision Tree) は分類規則を木で表したものです。 実物を見た方が早いので、先に決定木の作り方から説明します。
まず、訓練データから、入力 X と出力 y をnumpy.ndarrayで取り出します。
X = df_iris_train.drop('class', axis=1).values y = df_iris_train['class'].values
dropはDataFrameから行または列を取り除きます(axis オプションで行か列かを指定します)。 valuesはDataFrameをnumpy.ndarrayに変換します。
scikit-learnで決定木学習を使うには、sklearn.tree.DecisionTreeClassifierを使います。 fit関数で予測モデル(ここでは決定木)を学習します。
from sklearn.tree import DecisionTreeClassifier clf = DecisionTreeClassifier() clf.fit(X, y)
ここで、clf は classifier の略です。
学習したモデルのスコアを確認します。 sklearn.tree.DecisionTreeClassifierのスコアは、正解率 (mean accuracy) です。
clf.score(X, y)
学習した決定木の可視化 †
可視化にはGraphvizとPythonのpydotplusパッケージを使います。
Graphvizはグラフ描画ソフトウェアで、下記のサイトからダウンロードできます。 (macOS Sierraの場合、mountainlion版のgraphviz-2.36.0.pkgをダウンロードします。)
pydotplusパッケージがインストールされていない場合は、ターミナルでpip3を使ってインストールします。
$ conda install pydotplus
インストールができたら、Jupyter Notebook上でグラフを作成して描画します。
import pydotplus from IPython.display import Image from sklearn.externals.six import StringIO from sklearn.tree import export_graphviz dot = StringIO() export_graphviz(clf, out_file=dot, feature_names=df_iris_test.columns, class_names=df_iris_train['class'].unique(), filled=True, rounded=True,) graph = pydotplus.graph_from_dot_data(dot.getvalue()) Image(graph.create_png())
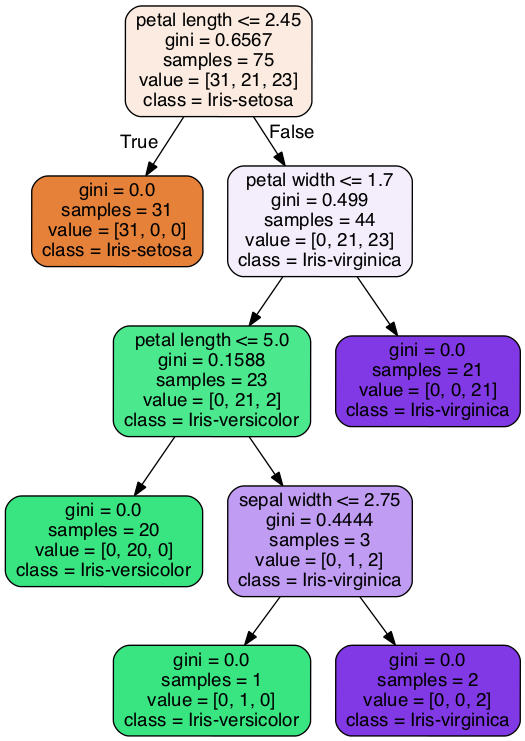
次のような決定木が表示されます。
決定木 †
決定木は、節 (node) と枝 (branch) から成ります。 一番上の節を根 (root) といいます。 根から枝が分かれて下へと伸びていきます。 先端の節を葉 (leaf) といいます。
節は条件にに対応します。 節の1行目にかかれているのが条件です。 条件が満たされるときは左の枝に、そうでないときは右の枝に進みます。 葉にたどり着いたら、その葉が表すクラスに分類します。 節の4行目に書かれているのが、その節で分類されるクラスです。
したがって、この決定木は、以下のようなルールを表していることになります。
- petal lengthの値が2.45以下ならば、Iris-setosa
- petal lengthの値が2.45より大きい、かつ、petal widthの値が1.7以下、かつ、petal lengthの値が5.0以下ならば、Iris-versicolor
- petal lengthの値が2.45より大きい、かつ、petal widthの値が1.7以下、かつ、petal lengthの値が5.0より大きい、かつ、sepal widthの値が2.75以下ならば、Iris-versicolor
- petal lengthの値が2.45より大きい、かつ、petal widthの値が1.7以下、かつ、petal lengthの値が5.0より大きい、かつ、sepal widthの値が2.75より大きいならば、Iris-virginica
- petal lengthの値が2.45より大きい、かつ、petal widthの値が1.7より大きいならば、Iris-virginica
決定木を学習するアルゴリズムでは、まず、条件を選びます。 説明変数が数値の場合は、訓練データに含まれている値の中から、訓練データを最もよく分割する値 [math]\theta[/math] を選び、「その変数の値が [math]\theta[/math] 以下である」という条件にします。
このとき「最もよく分割する」ことを評価する基準として、ジニ係数 (Gini index) と情報量利得 (information gain) があります。
ジニ係数 †
分類するクラスが [math]k[/math] 個のとき、クラス [math]i[/math] に分類される確率を [math]P_i[/math] とすると、ジニ係数 $G$ は以下のように求められます。 \[ G = 1 - \sum_{i=1}^{k} P_i^2 \]
クラス [math]i[/math] に分類される確率が [math]P_i = 1[/math] のとき、そのクラス以外のクラスに分類される確率は [math]P_j = 0[/math] になり、ジニ係数は 0 になります。
どのクラスにも均等に分類されるとき、すなわち、すべてのクラスにおいて [math]\displaystyle P_i = \frac{1}{k}[/math] のとき、ジニ係数は最大になります。
つまり、ジニ係数が小さいほど良いです。
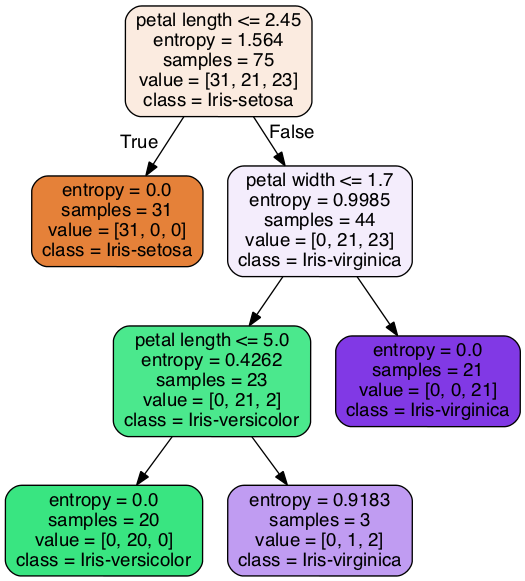
情報量利得 †
分類するクラスが [math]k[/math] このとき、クラス [math]i[/math] に分類される確率を [math]P_i[/math] とすると、平均情報量 (entropy) [math]H(P)[/math] が次のように求められます。 \[ H(P) = - \sum_{i=1}^{k} P_i \log P_i \]
クラス [math]i[/math] に分類される確率が [math]P_i = 1[/math] のとき、そのクラス以外のクラスに分類される確率は [math]P_j = 0[/math] になり、このときの平均情報量は 0 になります。
どのクラスにも均等に分類されるとき、すなわち、すべてのクラスにおいて [math]\displaystyle P_i = \frac{1}{k}[/math] のとき、平均情報量は最大になります。
つまり、平均情報量も小さいほど良いです。
情報量利得は、節の条件によって分割することによって平均情報量が減った量です。 分割後の平均情報量は、それぞれの節の平均情報量のデータ数に比例した重み付き平均によって求めます。
学習した決定木による予測 †
まず、テストデータの入力Xをnumpy.ndarray形式に変換します。
X = df_iris_test.values
ここでは、訓練データの入力Xを上書きしていますので、注意しましょう。
predictメソッドで学習したモデルに基づいてラベルを予測します。
p = clf.predict(X)
予測したラベルの出力 †
DeepAnalyticsでは、予測した結果をヘッダなしのCSV形式のファイルとしてアップロードします。
そこで、予測したラベルをCSV形式で出力します。 このとき、テストデータを参照してインデックスとします。
pd.DataFrame(p, index=df_iris_test.index).to_csv('predict.csv', header=False)
学習パラメーター †
上の例ではデフォルトの学習パラメーターで決定木を学習しましたが、学習パラメーターを指定するためのオプションがいくつか用意されています。
例えば、評価基準 (criterion) を情報量利得 (entropy) に、木の深さの最大値 (max_depth) を3にして実行すると、次のようになります。
clf = DecisionTreeClassifier(criterion='entropy', max_depth=3)
irisデータでは学習パラメーターを変更してもあまり効果がありませんが、実際のデータを分析するときには学習パラメーターを調整する必要があります。
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)