- バックアップ一覧
- 差分 を表示
- 現在との差分 を表示
- ソース を表示
- バイオ・データ・マイニング/Rで非線形回帰分析する へ行く。
- 1 (2015-02-01 (日) 11:36:18)
- 2 (2015-02-01 (日) 12:22:22)
このページは自分用のメモで,まだ書きかけです.
はじめに †
ここでは,Rを使って非線形回帰分析をします.
目的関数が線形の場合,最小二乗法を用いて残差 (RSS) が最小となるパラメーターを解析的に求めることができます. これから回帰分析をはじめる場合は,先に線形回帰分析をやってみましょう.
- Rで回帰分析する - とうごろうぃき
目的関数が非線形の場合,最小二乗法で解析的に解くことができません. そこで,ニュートン法や最急降下法のような方法を使って,残差 (RSS) が最小となるパラメーターを探索します. ここでは,Levenberg-Marquardt法を用います.
Levenberg-Marquardt法は,minpack.lmパッケージに含まれています.
非線形回帰 †
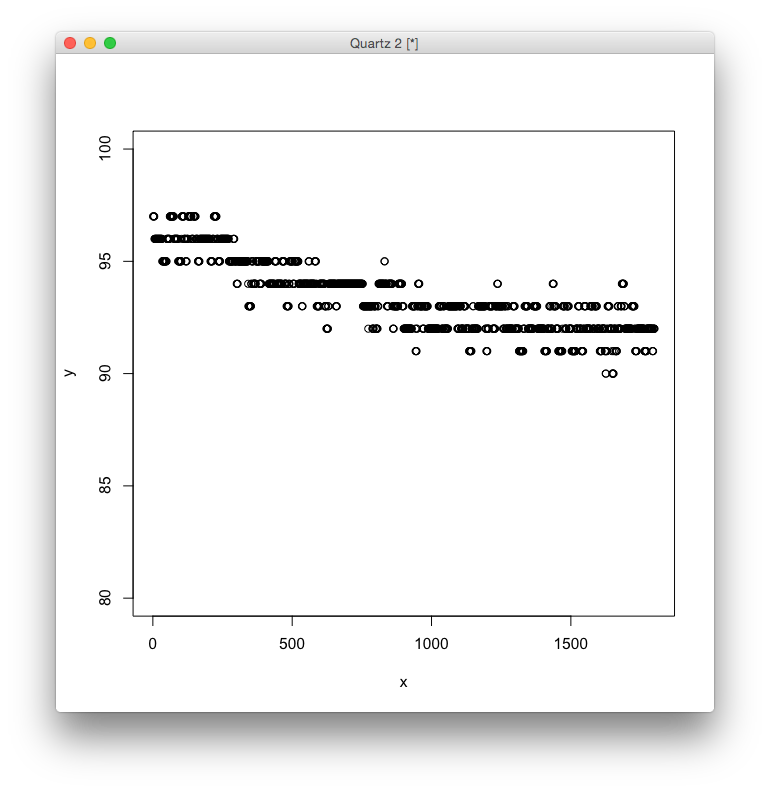
ここでは,次のようなデータに対して非線形回帰を行います.
> data <- read.csv("data.csv") > head(data) x y 1 1 97 2 2 97 3 3 97 4 4 97 5 5 97 6 6 96 > plot(x, y, ylim=c(80,100))
ここでは,モデルが次のような式で表される曲線を考えます. \[ y = a e^{bx} + c \]
> getPred <- function(parS, xx) parS$a * exp(xx * parS$b) + parS$c
![[PukiWiki] [PukiWiki]](https://xn--p8ja5bwe1i.jp:443/wiki/image/banner.png)